题目内容
过点(2-
,0)(n∈N*)且方向向量为(2,1)的直线交双曲线x2-y2=4于An,Bn两点,记原点为O,△OAnBn的面积为Sn,则
Sn= .
| 1 |
| n |
| lim |
| n→∞ |
考点:数列的极限
专题:综合题,圆锥曲线中的最值与范围问题
分析:依题意,可知过点(2-
,0)的直线的斜率为
,n→+∞时,点(2-
,0)→(2,0),原问题转化为直线x-2y-2=0与双曲线x2-y2=4的两个交点A、B与原点O所组成的三角形的面积,利用直线与圆锥曲线的位置关系,利用弦长公式、三角形的面积公式即可求得答案.
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
解答:
解:∵过点(2-
,0)(n∈N*)且方向向量为(2,1),即其斜率k=
,
(2-
)=2,
∴当n→+∞时,点(2-
,0)→(2,0),
∴n→+∞时,△OAnBn的面积就是直线y-0=
(x-2),即x-2y-2=0与双曲线x2-y2=4的两个交点A、B与原点O所组成的三角形的面积,设为S,
由
消去x得:3y2+8y=0,设A(x1,y1),B(x2,y2),
则y1+y2,=-
,y1•y2,=0,x1+x2,=2y1+2y2,+4=-
,
∴|AB|=
=
•
=
•
=
.
又O点到直线x-2y-2=0的距离d=
=
,
∴S=
Sn=
|AB|•d=
×
×
=
.
为Sn,
故答案为:
.
| 1 |
| n |
| 1 |
| 2 |
| lim |
| n→∞ |
| 1 |
| n |
∴当n→+∞时,点(2-
| 1 |
| n |
∴n→+∞时,△OAnBn的面积就是直线y-0=
| 1 |
| 2 |
由
|
则y1+y2,=-
| 8 |
| 3 |
| 4 |
| 3 |
∴|AB|=
| (x2-x1)2+(y2-y1)2 |
1+(
|
| (y2+y1)2-4y1y2 |
| 5 |
| 8 |
| 3 |
8
| ||
| 3 |
又O点到直线x-2y-2=0的距离d=
| |-2| | ||
|
| 2 | ||
|
∴S=
| lim |
| n→∞ |
| 1 |
| 2 |
| 1 |
| 2 |
8
| ||
| 3 |
| 2 | ||
|
| 8 |
| 3 |
为Sn,
故答案为:
| 8 |
| 3 |
点评:本题考查数列的极限,理解题意,求得
(2-
)=2,原问题转化为直线x-2y-2=0与双曲线x2-y2=4的两个交点A、B与原点O所组成的三角形的面积是关键,考查直线与圆锥曲线的位置关系,考查弦长公式,考查转化思想与综合运算能力.
| lim |
| n→∞ |
| 1 |
| n |

练习册系列答案
相关题目
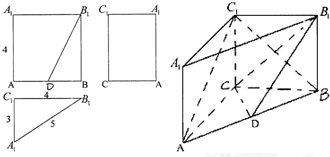
 如图,已知△ABC中,AB=AC=4,∠BAC=90°,D是BC的中点,若向量
如图,已知△ABC中,AB=AC=4,∠BAC=90°,D是BC的中点,若向量