题目内容
函数y=tan|x|的单调区间为 .
考点:正切函数的值域
专题:三角函数的图像与性质
分析:函数y=tan|x|为偶函数,它的图象关于原点对称,数形结合求得函数y=tan|x|的单调区间.
解答:
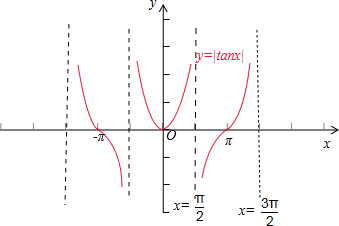 解:函数y=tan|x|为偶函数,它的图象关于原点对称,如图所示:
解:函数y=tan|x|为偶函数,它的图象关于原点对称,如图所示:
当x>0时,y=tanx,增区间为(0,
)∪(kπ-
,kπ+
),k∈N*.
当x<0时,y=-tanx,减区间为(-
,0)∪(kπ-
,kπ-
),k为非正整数.
故答案为:增区间为(0,
)∪(kπ-
,kπ+
),k∈N*;
减区间为(-
,0)∪(kπ-
,kπ-
),k为非正整数.
 解:函数y=tan|x|为偶函数,它的图象关于原点对称,如图所示:
解:函数y=tan|x|为偶函数,它的图象关于原点对称,如图所示:当x>0时,y=tanx,增区间为(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
当x<0时,y=-tanx,减区间为(-
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
故答案为:增区间为(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
减区间为(-
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
点评:本题主要考查正切函数的图象特征,正切函数的单调性,属于基础题.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若(2b-c)cosA=acosC,则A=( )
| A、30° | B、45° |
| C、60° | D、120° |
 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若BC=2BF,且AF=4,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若BC=2BF,且AF=4,则此抛物线的方程为