题目内容
3.设f(x)是定义在R上的奇函数,当x<0时,f(x)=-1-log2(-x).(1)求f(x)的解析式;
(2)设g(x)=2f(2x+3)-f(2x+1),若g(x)≥m恒成立,求实数m的最大值.
分析 (1)由奇函数的定义可得f(-x)=-f(x),f(0)=0,当x>0时,-x<0,由条件可得x>0的解析式,进而得到f(x)的解析式;
(2)化简g(x)的解析式,再由解不等式可得最小值,由恒成立思想可得m的范围,进而得到最大值.
解答 解:(1)f(x)是定义在R上的奇函数,即有f(-x)=-f(x),
f(0)=0,
当x>0时,-x<0,f(-x)=-1-log2x,即有f(x)=1+log2x.
则f(x)=$\left\{\begin{array}{l}{-1-lo{g}_{2}(-x),x<0}\\{0,x=0}\\{1+lo{g}_{2}x,x>0}\end{array}\right.$;
(2)由(1)可得g(x)=2(1+log2(2x+3))-(1+log2(2x+1))
=1+log2$\frac{({2}^{x}+3)^{2}}{{2}^{x}+1}$,
由$\frac{({2}^{x}+3)^{2}}{{2}^{x}+1}$=(2x+1)+$\frac{4}{{2}^{x}+1}$+4≥2$\sqrt{({2}^{x}+1)•\frac{4}{{2}^{x}+1}}$+4=8.
当且仅当x=0时,取得等号.
即有g(x)的最小值为1+log28=4,
由g(x)≥m恒成立可得m≤4,
则m的最大值为4.
点评 本题考查函数的奇偶性的运用和不等式恒成立问题,注意转化为求函数的最值问题,考查基本不等式和对数性质的运用,属于中档题.

练习册系列答案
相关题目
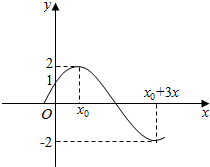 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图 