题目内容
5.7位同学站成一排.按下列要求各有多少种排列方法?(1)甲必须站在乙的左边;
(2)甲、乙和丙三个同学由左向右排列.
分析 (1)定序法,甲乙的顺序只有两种,7名同学站成一排,排法数为${A}_{7}^{7}$,问题得以解决;
(2)定序法,甲乙丙的顺序有6种,7名同学站成一排,排法数为${A}_{7}^{7}$,问题得以解决.
解答 解:(1)甲同学必须站在乙同学的左边(不一定相邻),7名同学站成一排,排法数为${A}_{7}^{7}$,其中甲同学站在乙同学的左边和乙同学站在甲同学的左边(不一定相邻)的情况一一对应,
各占其半,故满足条件的排法总数为$\frac{{A}_{7}^{7}}{2}$=2520种.
(2)同(1)可得,有${A}_{7}^{7}$÷${A}_{3}^{3}$=840种.
点评 本题考查排列、组合的应用,注意特殊问题的处理方法,如相邻用捆绑法,不能相邻用插空法,定序法,属于中档题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
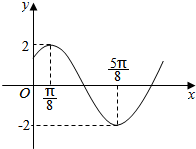 已知函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示:
已知函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示: