题目内容
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。
(Ⅰ)若∠PAB=30°,求以MN为直径的圆方程;
(Ⅱ)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
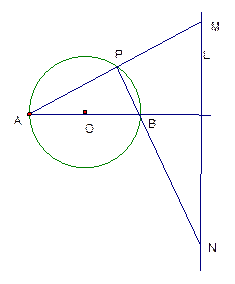
(Ⅰ)若∠PAB=30°,求以MN为直径的圆方程;
(Ⅱ)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。

解:建立如图所示的直角坐标系,
⊙O的方程为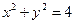 ,
,
直线L的方程为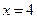 。
。
(Ⅰ)∵∠PAB=30°,∴点P的坐标为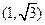 ,
,
∴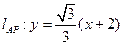 ,
,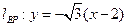 。
。
将x=4代入,得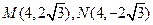 。
。
∴MN的中点坐标为(4,0),MN=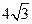 。
。
∴以MN为直径的圆的方程为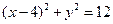 。
。
同理,当点P在x轴下方时,所求圆的方程仍是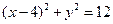 。
。
(Ⅱ)设点P的坐标为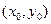 ,∴
,∴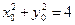 (
(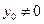 ),∴
),∴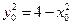 。
。
∵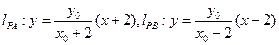 ,
,
将x=4代入,得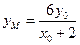 ,
,
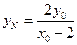 。∴
。∴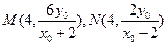 ,MN=
,MN=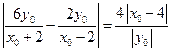 。
。
MN的中点坐标为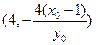 。
。
以MN为直径的圆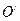 截x轴的线段长度为
截x轴的线段长度为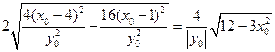
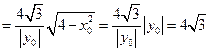 为定值。
为定值。
∴⊙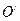 必过⊙O 内定点
必过⊙O 内定点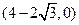 。
。
⊙O的方程为
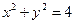 ,
,直线L的方程为
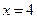 。
。(Ⅰ)∵∠PAB=30°,∴点P的坐标为
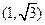 ,
,∴
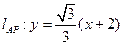 ,
,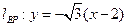 。
。将x=4代入,得
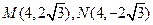 。
。∴MN的中点坐标为(4,0),MN=
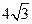 。
。∴以MN为直径的圆的方程为
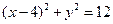 。
。同理,当点P在x轴下方时,所求圆的方程仍是
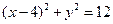 。
。(Ⅱ)设点P的坐标为
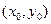 ,∴
,∴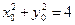 (
(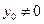 ),∴
),∴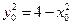 。
。∵
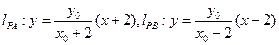 ,
,将x=4代入,得
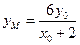 ,
,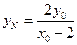 。∴
。∴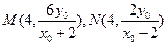 ,MN=
,MN=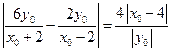 。
。MN的中点坐标为
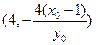 。
。以MN为直径的圆
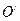 截x轴的线段长度为
截x轴的线段长度为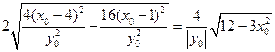
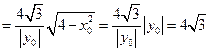 为定值。
为定值。∴⊙
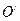 必过⊙O 内定点
必过⊙O 内定点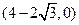 。
。略

练习册系列答案
相关题目
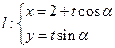 (
(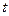 为参数),圆
为参数),圆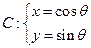 (
(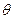 为参数).
为参数).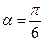 时,试判断直线
时,试判断直线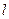 与圆
与圆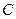 的位置关系;
的位置关系;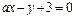 与圆
与圆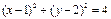 相交于
相交于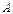 、
、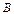 两点,且弦
两点,且弦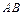 的长为
的长为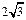 ,则
,则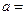 ____________.
____________.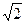
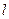 经过坐标原点,且与圆
经过坐标原点,且与圆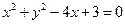 相切,切点在第四象限,则直线
相切,切点在第四象限,则直线