题目内容
19.(本小题满分8分)已知,过点M(-1,1)的直线l被圆C:x2 + y2-2x + 2y-14 = 0所截得的弦长为4,求直线l的方程.
解:由圆的方程可求得圆心C的坐标为(1,-1),半径为4
∵直线l被圆C所截得的弦长为4
∴圆心C到直线l的距离为2
(1)若直线l的斜率不存在,则直线l的方程为x =-1,此时C到l的距离为2,可求得弦长为4,符合题意。
(2)若直线l的斜率存在,设为k, 则直线l的方程为y-1 = k(x + 1)
即kx-y + k + 1 =" 0," ∵圆心C到直线l的距离为2
∴ =" 2 " ∴k2 + 2k + 1 = k2 + 1
∴k =" 0 " ∴直线l的方程为y =1
综上(1)(2)可得:直线l的方程为x =-1或 y =1.
∵直线l被圆C所截得的弦长为4
∴圆心C到直线l的距离为2
(1)若直线l的斜率不存在,则直线l的方程为x =-1,此时C到l的距离为2,可求得弦长为4,符合题意。
(2)若直线l的斜率存在,设为k, 则直线l的方程为y-1 = k(x + 1)
即kx-y + k + 1 =" 0," ∵圆心C到直线l的距离为2
∴ =" 2 " ∴k2 + 2k + 1 = k2 + 1
∴k =" 0 " ∴直线l的方程为y =1
综上(1)(2)可得:直线l的方程为x =-1或 y =1.
略

练习册系列答案
相关题目
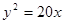 的焦点为圆心,且与双曲线
的焦点为圆心,且与双曲线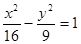 的两条渐近线都相切的圆的方程为
的两条渐近线都相切的圆的方程为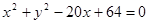
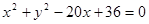
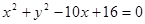

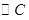 经过原点且与两坐标轴分别交于点A与点B,点A的坐标为
经过原点且与两坐标轴分别交于点A与点B,点A的坐标为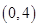 ,M是圆上一点,
,M是圆上一点,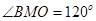 ,则圆心C的坐标
,则圆心C的坐标 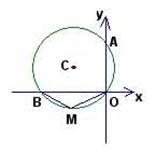




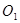 方程为
方程为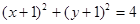 ,圆
,圆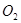 方程为
方程为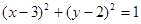 ,则方程
,则方程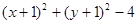
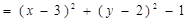 表示的轨迹是 ( )
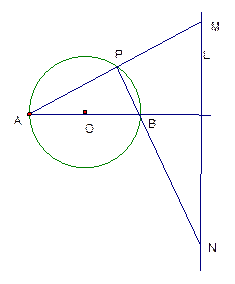
表示的轨迹是 ( ) 的直线
的直线 的中垂线
的中垂线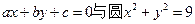 相交于两点M,N,若
相交于两点M,N,若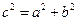 ,则
,则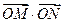 (O为坐标原点)等于 ( )
(O为坐标原点)等于 ( )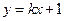 与圆
与圆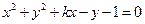 的两个交点恰好关于
的两个交点恰好关于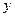 轴
轴 对称,则
对称,则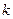 等于( )
等于( )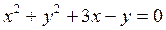 和
和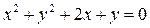 的交点的直线方程 ;
的交点的直线方程 ;