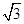题目内容
过点A(11,2)作圆x2+y2+2x-4y-164=0的弦,其中弦长为整数的共有( )
| A.16条 | B.17条 | C.32条 | D.34条 |
C
∵圆的标准方程为:(x+1)2+(y-2)2=132,则圆心为C(-1,2),半径为r=13.∵|CA|=12,∴经过A点且垂直于CA的弦是经过A的最短的弦,其长度为2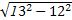 =10;而经过A点的最长的弦为圆的直径2r=26;
=10;而经过A点的最长的弦为圆的直径2r=26;
∴经过A点且为整数的弦长还可以取11,12,13,14,…,25共15个值,又由圆内弦的对称性知,经过某一点的弦的长若介于最大值与最小值之间,则一定有2条,而最长的弦与最短的弦各只有1条,故一共有15×2+2=32(条).
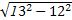 =10;而经过A点的最长的弦为圆的直径2r=26;
=10;而经过A点的最长的弦为圆的直径2r=26;∴经过A点且为整数的弦长还可以取11,12,13,14,…,25共15个值,又由圆内弦的对称性知,经过某一点的弦的长若介于最大值与最小值之间,则一定有2条,而最长的弦与最短的弦各只有1条,故一共有15×2+2=32(条).

练习册系列答案
相关题目
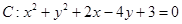 .
.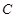 的切线在
的切线在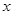 轴和
轴和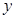 轴上的截距相等,且截距不为零,求此切线的方程;
轴上的截距相等,且截距不为零,求此切线的方程;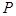 向该圆引一条切线,切点为
向该圆引一条切线,切点为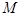 ,
,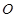 为坐标原点,且有
为坐标原点,且有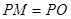 ,求使
,求使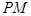 的长取得最小值的点
的长取得最小值的点 与直线
与直线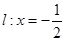 相切且与圆
相切且与圆 :
: 外切。
外切。 方程;
方程; 作直线
作直线 交轨迹
交轨迹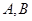 两点,
两点, 是
是 点关于坐标原点
点关于坐标原点 的对称点,求证:
的对称点,求证: ;
; =6,求圆C的方程.
=6,求圆C的方程.
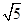 的点的个数是________.
的点的个数是________.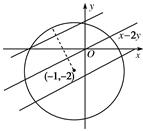
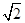 =0,则圆C被直线l所截得的弦长为( )
=0,则圆C被直线l所截得的弦长为( )