题目内容
已知动圆 与直线
与直线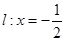 相切且与圆
相切且与圆 :
: 外切。
外切。
(1)求圆心 的轨迹
的轨迹 方程;
方程;
(2)过定点 作直线
作直线 交轨迹
交轨迹 于
于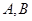 两点,
两点, 是
是 点关于坐标原点
点关于坐标原点 的对称点,求证:
的对称点,求证: ;
;
 与直线
与直线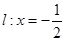 相切且与圆
相切且与圆 :
: 外切。
外切。(1)求圆心
 的轨迹
的轨迹 方程;
方程;(2)过定点
 作直线
作直线 交轨迹
交轨迹 于
于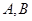 两点,
两点, 是
是 点关于坐标原点
点关于坐标原点 的对称点,求证:
的对称点,求证: ;
;(1) ;(2)详见解析.
;(2)详见解析.
 ;(2)详见解析.
;(2)详见解析.试题分析:(1)令
 点坐标为
点坐标为 ,
, ,动圆得半径为
,动圆得半径为 ,则根据两圆相外切及直线
,则根据两圆相外切及直线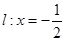 与圆相切得性质可得,
与圆相切得性质可得, ,
, ,即
,即 ,即
,即 ,化简可求动圆圆心
,化简可求动圆圆心 的轨迹C的方程,也可根据题意动圆圆心
的轨迹C的方程,也可根据题意动圆圆心 到定点
到定点 和到定直线
和到定直线 的距离相等,由抛物线的定义可直接求;(2)求证:
的距离相等,由抛物线的定义可直接求;(2)求证: ;由题意是
;由题意是 点关于坐标原点
点关于坐标原点 的对称点,设直线
的对称点,设直线 的斜率分别为
的斜率分别为 ,只要证明
,只要证明 ,即证
,即证 即可,因此可设直线
即可,因此可设直线 的方程为
的方程为
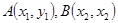 ,将直线方程代入
,将直线方程代入 得,
得, ,有根与系数关系
,有根与系数关系 ,可证得
,可证得 .
.试题解析:(1)法1:根据题意动圆圆心
 到定点
到定点 和到定直线
和到定直线 的距离相等,根据抛物线的定义可知,动圆圆心
的距离相等,根据抛物线的定义可知,动圆圆心 的轨迹C的方程为
的轨迹C的方程为 . 5分
. 5分法2:设
 ,则
,则 ,即
,即 得
得 . 5分
. 5分(2)依题意,设直线
 的方程为
的方程为
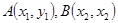 ,则
,则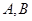 两点的坐标满足方程组:
两点的坐标满足方程组: 消去并
消去并 整理,得
整理,得 ,
,
设直线AE和BE的斜率分别为
 ,则:
,则:




练习册系列答案
相关题目
 :
: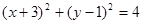 和圆
和圆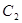 :
: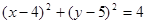
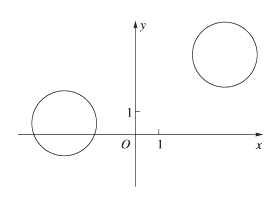
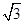 ,求直线l的方程;
,求直线l的方程;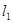 和
和 ,它们分别与圆
,它们分别与圆 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ). 被圆
被圆 所截得的弦长为________.
所截得的弦长为________. 上恰有两点到直线
上恰有两点到直线 (
( 的距离等于1,则
的距离等于1,则 的取值范围为
的取值范围为 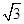 y-2
y-2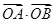 =( ).
=( ).