题目内容
1.已知等比数列{an}中,a2=$\frac{1}{9}$,a3+a4=$\frac{4}{81}$,且a1>a2.(1)求数列{an}的前n项和Sn;
(2)设bn=log3(a1a2)+log3(a2a3)+…+log3(anan+1),求数列{bn}的通项公式.
分析 (1)通过a2=$\frac{1}{9}$、a3+a4=$\frac{4}{81}$=a2(q+q2),可得公比,进而可得结论;
(2)通过(1)可知an=$\frac{1}{{3}^{n}}$,进而anan+1=$\frac{1}{{3}^{2n+1}}$,利用对数的性质计算即可.
解答 解:(1)∵a2=$\frac{1}{9}$,
∴a3+a4=$\frac{4}{81}$=a2(q+q2),
∴q=$\frac{1}{3}$或-$\frac{4}{3}$(舍),
∴a1=$\frac{{a}_{2}}{q}$=$\frac{\frac{1}{9}}{\frac{1}{3}}$=$\frac{1}{3}$,
∴Sn=$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$=$\frac{1}{2}$-$\frac{1}{2}$•$\frac{1}{{3}^{n}}$;
(2)由(1)可知an=$\frac{1}{3}•\frac{1}{{3}^{n-1}}$=$\frac{1}{{3}^{n}}$,
∴anan+1=$\frac{1}{{3}^{n}}$•$\frac{1}{{3}^{n+1}}$=$\frac{1}{{3}^{2n+1}}$,
∴bn=log3(a1a2)+log3(a2a3)+…+log3(anan+1)
=log3$\frac{1}{{3}^{3}}$+log3$\frac{1}{{3}^{5}}$+…+log3$\frac{1}{{3}^{2n+1}}$
=-3-5-…-(2n+1)
=-$\frac{n(3+2n+1)}{2}$
=-n(n+2).
点评 本题考查求数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | a≤2 | B. | a≥2 | C. | a≤1 | D. | a≥1 |
| A. | x=-$\frac{π}{4}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=-$\frac{π}{2}$ |
 把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列,(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )
把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列,(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )| A. | 第63行第2列 | B. | 第62行第12列 | C. | 第64行第30列 | D. | 第64行第60列 |
| A. | 0.9 | B. | 0.2 | C. | 0.7 | D. | 0.5 |
①|x+$\frac{1}{x}$|的最小值是2 ②$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$的最小值是2 ③log2x+logx2的最小值是2 ④3x+3-x的最小值是2.
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
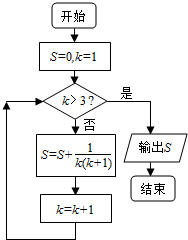
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |