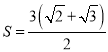Question

【题目】已知函数f（x）=Asin（ωx+）（A＞0，ω＞0，||＜π），在同一周期内，当 时，f（x）取得最大值3；当 时，f（x）取得最小值﹣3．
（1）求函数f（x）的解析式和图象的对称中心；
（2）若 时，关于x的方程2f（x）+1﹣m=0有且仅有一个实数解，求实数m的取值范围．

Answer 1

【答案】
（1）解：由题意可知A=3，

∵在同一周期内，当 时，f（x）取得最大值3；当 时，f（x）取得最小值﹣3．

∴ T=

∴ ，

∴ω=2．

又∵

得 ，

∵||＜π，

解得 ，

∴函数f（x）的解析式 ．

令 得

∴图象的对称中心为 ，（k∈Z）．

（2）解：由（1）知 ．

那么：方程2f（x）+1﹣m=0等价于 在 上有且仅有一个实数解

∵ ，

∴ ，

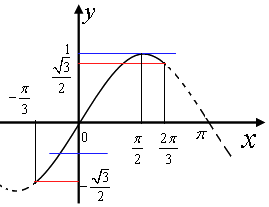
令函数y1=sinu，则u∈ ，其图象为：

结合函数图象有， 或

解得：m=7或 ．

实数m的取值范围为m=7或 ．

【解析】（1）根据三角函数的性质可得A，当 时，f（x）取得最大值3；当 时，f（x）取得最小值﹣3．求解周期T，可得ω图象过（ ，0），带入求解，可得f（x）解析式，令ωx+=kπ，求解对称中心．（2）将f（x）的解析式带入化简，求解 时，画出f（x）的图象，利用数形结合法，可得实数m的取值范围．
【考点精析】本题主要考查了正弦函数的对称性的相关知识点，需要掌握正弦函数的对称性：对称中心；对称轴才能正确解答此题．