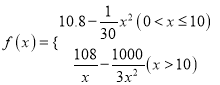Question

【题目】已知函数y=f（x），若在定义域内存在x0 ， 使得f（﹣x0）=﹣f（x0）成立，则称x0为函数f（x）的局部对称点．
（1）若a∈R，a≠0，证明：函数f（x）=ax2+x﹣a必有局部对称点；
（2）若函数f（x）=2x+b在区间[﹣1，1]内有局部对称点，求实数b的取值范围；
（3）若函数f（x）=4x﹣m2x+1+m2﹣3在R上有局部对称点，求实数m的取值范围．

Answer 1

【答案】
（1）证明：∵f（x）=ax2+x﹣a，∴f（﹣x）=ax2﹣x﹣a，

令f（﹣x）=﹣f（x）得ax2﹣x﹣a=﹣ax2﹣x+a，化简得ax2﹣a=0（a≠0），

∵△=4a2＞0恒成立，

∴方程f（﹣x）=﹣f（x）必定有解，即函数f（x）=ax2+x﹣a必有局部对称点．

（2）解：f（x）=2x+b，f（﹣x）=2﹣x+b，

令f（﹣x）=﹣f（x）得2x+2﹣x=﹣2b，即b=﹣ （2x+2﹣x），

令2x=t，g（t）=﹣ （t+ ），∵x∈[﹣1，1]，∴ ，

∴g′（t）=﹣ + ，令g′（t）=0得t=1或t=﹣1（舍）．

当 ≤t＜1时，g′（t）＞0，当1＜t≤2时，g′（t）＜0，

∴g（t）在[ ，1]上单调递增，在（1，2]单调递减，

∵g（ ）=﹣ ，g（1）=﹣1，g（2）=﹣ ，

∴g（t）的最大值为﹣1，g（t）的最小值为﹣ ．

∴b的取值范围是 ．

（3）解：f（x）=4x﹣m2x+1+m2﹣3，f（﹣x）=4﹣x﹣m2﹣x+1+m2﹣3，

令f（﹣x）=﹣f（x）得4x+4﹣x﹣2m（2x+2﹣x）+2（m2﹣3）=0（*），

∵f（x）=4x﹣m2x+1+m2﹣3在R上有局部对称点，

∴4x+4﹣x﹣2m（2x+2﹣x）+2（m2﹣3）=0在R上有解．

令2x+2﹣x=t，则t∈[2，+∞），4x+4﹣x=t2﹣2，

∴关于t的方程t2﹣2mt+2m2﹣8=0在t∈[2，+∞）上有解，

令h（t）=t2﹣2mt+2m2﹣8，则h（2）=2m2﹣4m﹣4≤0或 ．

解得： 或 ，即1﹣ ≤m≤2 ．

∴m的取值范围是[1﹣ ，2 ]．

【解析】（1）令f（﹣x）=﹣f（x）得出关于x的方程，根据判别式证明方程有解即可；（2）令f（﹣x）=﹣f（x）得出关于x的方程，令t=2x得出b关于t的函数g（t），求出函数g（t）在[ ，2]上的值域即可；（3）令f（﹣x）=﹣f（x）得出关于x的方程，令2x+2﹣x=t得出关于t的一元二次方程在[2，+∞）上有解，根据二次函数的性质不等式方程组求出m的范围．