题目内容
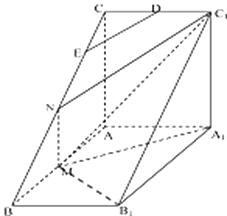
【题目】如图,直三棱柱ABC﹣A1B1C1中,AC⊥AB,AB=2AA1 , M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
(Ⅰ)若DE∥平面A1MC1 , 求 ![]() ;
;
(Ⅱ)求直线BG和平面A1MC1所成角的余弦值.
【答案】解:(Ⅰ)取BC中点N,连结MN,C1N, ∵M,N分别为AB,CB中点
∴MN∥AC∥A1C1 ,
∴A1 , M,N,C1四点共面,
且平面BCC1B1∩平面A1MNC1=C1N,
又DE∩平面BCC1B1 ,
且DE∥平面A1MC1 , ∴DE∥C1N,
∵D为CC1的中点,∴E是CN的中点,
∴ ![]() =
= ![]() .
.
(Ⅱ)连结B1M,
因为三棱柱ABC﹣A1B1C1为直三棱柱,∴AA1⊥平面ABC,
∴AA1⊥AB,即四边形ABB1A1为矩形,且AB=2AA1 ,
∵M是AB的中点,∴B1M⊥A1M,
又A1C1⊥平面ABB1A1 ,
∴A1C1⊥B1M,从而B1M⊥平面A1MC1
∴MC1是B1C1在平面A1MC1内的射影,
∴B1C1与平面A1MC1所成的角为∠B1C1M,
又B1C1∥BC,
∴直线BC和平面A1MC1所成的角即B1C1与平面A1MC1所成的角
设AB=2AA1=2,且三角形A1MC1是等腰三角形
∴A1M=A1C1= ![]() ,则MC1=2,B1C1=
,则MC1=2,B1C1= ![]() ,
,
∴cos∠B1C1M= ![]() ,∴直线BC和平面A1MC1所成的角的余弦值为
,∴直线BC和平面A1MC1所成的角的余弦值为 ![]() .
. 
【解析】(Ⅰ)取BC中点N,连结MN,C1N,由已知得A1 , M,N,C1四点共面,由已知条件推导出DE∥C1N,从而求出 ![]() .(Ⅱ)连结B1M,由已知条件得四边形ABB1A1为矩形,B1C1与平面A1MC1所成的角为∠B1C1M,由此能求出直线BC和平面A1MC1所成的角的余弦值.
.(Ⅱ)连结B1M,由已知条件得四边形ABB1A1为矩形,B1C1与平面A1MC1所成的角为∠B1C1M,由此能求出直线BC和平面A1MC1所成的角的余弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则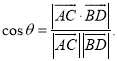 .
.

【题目】某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
周销售量 | 2 | 3 | 4 |
频数 | 20 | 50 | 30 |
(1)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(2)已知每吨该商品的销售利润为2千元,ξ表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求ξ的分布列和数学期望.