题目内容
【题目】在四菱锥P﹣ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
(I)求证:PA⊥AB;
(II)求直线AD与平面PCD所成角的大小.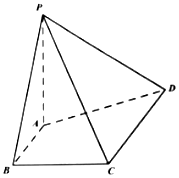
【答案】证明:(I)取CD的中点E,连接AE,PE,则AE⊥CD,PE⊥CD, ∵AE∩PE=E,∴CD⊥平面PAE.
∵PA平面PAE,∴CD⊥PA,
∵PA⊥AD,AD∩CD=D,
∴PA⊥平面ABCD,
∵AB平面ABCD,
∴PA⊥AB;
(II)解:由题意,AD=PE= ![]() .
.
设A到平面PCD的距离为h,则由等体积可得 ![]() =
= ![]() ,
,
∴h= ![]()
∴直线AD与平面PCD所成角的正弦值为 ![]() =
= ![]() ,大小为30°.
,大小为30°.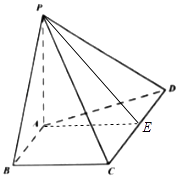
【解析】(I)取CD的中点E,连接AE,PE,则AE⊥CD,PE⊥CD,证明PA⊥平面ABCD,即可证明:PA⊥AB;(II)求出A到平面PCD的距离,即可求直线AD与平面PCD所成角的大小.
【考点精析】关于本题考查的直线与平面垂直的性质和空间角的异面直线所成的角,需要了解垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则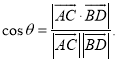 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目

