Question

【题目】广播电台为了了解某地区的听众对某个戏曲节目的收听情况，随机抽取了100名听众进行调查，下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图，将日均收听该节目时间不低于40分钟的听众成为“戏迷”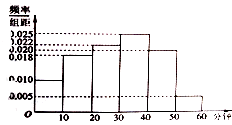

（1）根据已知条件完成2×2列联表，并判断“戏迷”与性别是否有关？

	“戏迷”	非戏迷	总计
男
女	10		55
总计

附：K2= ，

P（K2≥k）	0.05	0.01
k	3.841	6.635

（2）将上述调查所得到的频率当作概率．现在从该地区大量的听众中，采用随机抽样的方法每次抽取1名听众，抽取3次，记被抽取的3名听众中“戏迷”的人数为X，若每次抽取的结果相互独立，求X的分布列，数学期望及方差．

Answer 1

【答案】
（1）解：由频率分布直方图可知在抽取的100人中，“戏迷”有（0.02+0.005）×10×100=25人，

“戏迷”有25人，

2×2列联表如下：

	“戏迷”	非戏迷	总计
男	15	30	45
女	10	45	55
总计	25	75	100

将2×2列联表中的数据代入公式：

K2= ，

= ≈3.030＜3.841，

故没有理由认为“戏迷”与性别有关

（2）解：由题可知抽到“戏迷”的概率为0.25，

由题意可知X～B（3， ），

X	0	1	2	3
P

∴数学期望E（X）=np=3× = ，

方差D（X）=np（1﹣p）=3× × =

【解析】（1）由频率分布直方图求得“戏迷”有25人，完成2×2列联表，根据2×2列联表，代入求临界值的公式，求出观测值，利用观测值同临界值表进行比较，K2≈3.030＜3.841，故没有理由认为“戏迷”与性别有关；（2）由题意可知X～B（3， ），根据二项分布求得其分布列，数学期望及方差．
【考点精析】认真审题，首先需要了解离散型随机变量及其分布列(在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列)．