题目内容
【题目】已知函数f (x)= ![]() 的定义域集合是A,函数g(x)=lg[x2﹣(2a+1)x+a2+a]的定义域集合是B.
的定义域集合是A,函数g(x)=lg[x2﹣(2a+1)x+a2+a]的定义域集合是B.
(1)求集合A,B.
(2)若A∪B=B,求实数a的取值范围.
【答案】
(1)解:由题意 ![]() 所以 A={x|x≤﹣1或x>2};
所以 A={x|x≤﹣1或x>2};
x2﹣(2a+1)x+a2+a>0 B={x|x<a或x>a+1}
(2)解:由A∪B=B得AB,
因此 ![]()
解得:﹣1<a≤1,
∴实数a的取值范围是(﹣1,1]
【解析】(1)被开方数≥0,求A,对数的真数>0求出B.(2)由题意A是B的子集,可解出实数a的取值范围.
【考点精析】掌握集合的并集运算和函数的定义域及其求法是解答本题的根本,需要知道并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立;求函数的定义域时,一般遵循以下原则:①
B,反之也成立;求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷” 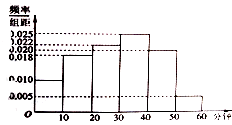
(1)根据已知条件完成2×2列联表,并判断“戏迷”与性别是否有关?
“戏迷” | 非戏迷 | 总计 | |
男 | |||
女 | 10 | 55 | |
总计 |
附:K2= ![]() ,
,
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
(2)将上述调查所得到的频率当作概率.现在从该地区大量的听众中,采用随机抽样的方法每次抽取1名听众,抽取3次,记被抽取的3名听众中“戏迷”的人数为X,若每次抽取的结果相互独立,求X的分布列,数学期望及方差.