题目内容
【题目】已知函数y=f(x)满足f(x﹣1)=2x+3a,且f(a)=7.
(1)求函数f(x)的解析式;
(2)若g(x)=xf(x)+λf(x)+x在[0,2]上最大值为2,求实数λ的值.
【答案】
(1)解:f(x﹣1)=2x+3a=2(x﹣1)+3a+2,
则f(x)=2x+3a+2,
∵f(a)=7,
∴2a+3a+2=7,
解得a=1,
∴f(x)=2x+5
(2)解:g(x)=xf(x)+λf(x)+x=x(2x+5)+2λx+5λ=2x2+(6+2λ)x+5λ,
则其对称轴为x=﹣ ![]() ,
,
当﹣ ![]() ≤0时,即λ≥﹣3时,函数g(x)在[0,2]上单调递增,故g(x)max=g(2)=9λ+20,
≤0时,即λ≥﹣3时,函数g(x)在[0,2]上单调递增,故g(x)max=g(2)=9λ+20,
当﹣ ![]() ≥2时,即λ≤﹣7时,函数g(x)在[0,2]上单调递减,故g(x)max=g(0)=5λ,
≥2时,即λ≤﹣7时,函数g(x)在[0,2]上单调递减,故g(x)max=g(0)=5λ,
当0<﹣ ![]() ≤1时,即﹣5≤λ<﹣3时,g(x)max=g(2)=9λ+20,
≤1时,即﹣5≤λ<﹣3时,g(x)max=g(2)=9λ+20,
当1<﹣ ![]() <2时,即﹣7<λ<﹣5时,g(x)max=g(0)=5λ,
<2时,即﹣7<λ<﹣5时,g(x)max=g(0)=5λ,
故,当λ≥﹣5时,g(x)max=g(2)=9λ+20=2,解得λ=﹣2,
当λ<﹣5时,g(x)max=g(0)=5λ=2,解的λ= ![]() ,舍去
,舍去
综上所述λ的值为﹣2
【解析】(1)根据配凑法即可求出函数的解析式,(2)化简g(x),根据二次函数的性质,分类讨论即可求出λ的值,
【考点精析】利用函数的最值及其几何意义对题目进行判断即可得到答案,需要熟知利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

 寒假学与练系列答案
寒假学与练系列答案【题目】已知函数f(x)=x2+bx+c满足f(2﹣x)=f(2+x),f(0)>0,且f(m)=f(n)=0(m≠n),则log4m﹣ ![]() n的值是( )
n的值是( )
A.小于1
B.等于1
C.大于1
D.由b的符号确定
【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于![]() 为合格品,小于
为合格品,小于![]() 为次品.现随机抽取这种芯片共
为次品.现随机抽取这种芯片共![]() 件进行检测,检测结果统计如表:
件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
芯片数量(件) |
|
|
|
|
|
已知生产一件芯片,若是合格品可盈利![]() 元,若是次品则亏损
元,若是次品则亏损![]() 元.
元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产![]() 件芯片所获得的利润不少于
件芯片所获得的利润不少于![]() 元的概率.
元的概率.
(Ⅱ)记![]() 为生产
为生产![]() 件芯片所得的总利润,求随机变量
件芯片所得的总利润,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
【题目】广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷” 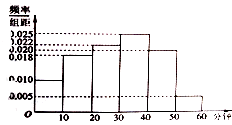
(1)根据已知条件完成2×2列联表,并判断“戏迷”与性别是否有关?
“戏迷” | 非戏迷 | 总计 | |
男 | |||
女 | 10 | 55 | |
总计 |
附:K2= ![]() ,
,
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
(2)将上述调查所得到的频率当作概率.现在从该地区大量的听众中,采用随机抽样的方法每次抽取1名听众,抽取3次,记被抽取的3名听众中“戏迷”的人数为X,若每次抽取的结果相互独立,求X的分布列,数学期望及方差.