题目内容
【题目】已知函数f(x)=x﹣alnx+ ![]() .
.
(1)若a=1,求f(x)在x∈[1,3]的最值;
(2)求函数f(x)的单调区间;
(3)若存在x0∈[1,e],使得f(x0)<0成立,求a的取值范围.
【答案】
(1)解:由题意知 ![]() ,x∈[1,3].
,x∈[1,3].
![]() ,
,
令f'(x)=0,x1=2,x2=﹣1(舍).
x | 1 | (1,2) | 2 | (2,3) | 3 |
f'(x) | ﹣2 | 为负 | 0 | 为正 |
|
f(x) | 3 | 递减 | 极小值 | 递增 |
|
由上表可知,函数f(x)的最小值为f(2)=2﹣ln2,函数f(x)的最大值为f(1)=3.
(2)解: ![]() ,令f'(x)=0,x1=﹣1,x2=1+a.
,令f'(x)=0,x1=﹣1,x2=1+a.
由于函数f(x)的定义域为(0,+∞),
当1+a≤0时,f'(x)>0,
当1+a>0时,0<x<1+a有f'(x)<0,x>1+a有f'(x)>0.
所以,当a≤﹣1时,函数f(x)的递增区间是(0,+∞);
当a>﹣1时,函数f(x)的递减区间是(0,1+a);递增区间是[1+a,+∞).
(3)解:当1+a≤1时,即a≤0时,函数f(x)在[1,e]上单调递增,f(1)<0解得a<﹣2;
当1+a≥e时,即a≥e﹣1时,函数f(x)在[1,e]上单调递减,f(e)<0解得 ![]() ;
;
当1<1+a<e时,即0<a<e﹣1时,函数f(x)在[1,1+a]上单调递减,[1+a,e]上单调递增,
∴f(1+a)=2+a﹣aln(1+a)<0,由于0<ln(1+a)<1,
所以a>aln(1+a),因此2+a﹣aln(1+a)>2,不等式f(1+a)<0无解.
综上所述,a<﹣2或 ![]()
【解析】(1)代入a值,利用导函数直接判断;(2)求导,在定义域内对a进行分类讨论;(3)使得f(x0)<0成立,只需求出区间内的最小值即可,对a进行分类讨论,求出函数的最小值.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
【题目】已知函数f(x)=x2+bx+c满足f(2﹣x)=f(2+x),f(0)>0,且f(m)=f(n)=0(m≠n),则log4m﹣ ![]() n的值是( )
n的值是( )
A.小于1
B.等于1
C.大于1
D.由b的符号确定
【题目】广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷” 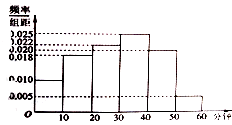
(1)根据已知条件完成2×2列联表,并判断“戏迷”与性别是否有关?
“戏迷” | 非戏迷 | 总计 | |
男 | |||
女 | 10 | 55 | |
总计 |
附:K2= ![]() ,
,
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
(2)将上述调查所得到的频率当作概率.现在从该地区大量的听众中,采用随机抽样的方法每次抽取1名听众,抽取3次,记被抽取的3名听众中“戏迷”的人数为X,若每次抽取的结果相互独立,求X的分布列,数学期望及方差.