题目内容
【题目】如图,在直角梯形ABCD中AD∥BC,∠ADC=90°,平面ABCD外一点P在平面ABCD内的射影Q恰在边AD上, PA=AD=2 BC=2,CD=.
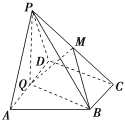
(1)若平面PQB⊥平面PAD,求证:Q为线段AD中点;
(2)在(1)的条件下,若M在线段PC上,且PA∥平面BMQ,求点M到平面PAB的距离.
【答案】(1)见解析;(2)![]()
【解析】(1)证明:∵P在平面ABCD内的射影Q恰在边AD上,
∴PQ⊥平面ABCD,
∵BQ![]() 平面ABCD,∴PQ⊥BQ,(2分)
平面ABCD,∴PQ⊥BQ,(2分)
∵PQB⊥平面PAD,且平面PQB∩平面PAD =PQ,
∴BQ⊥平面PAD.
∵AD![]() 平面PAD,∴BQ⊥AD.(4分)
平面PAD,∴BQ⊥AD.(4分)
∵∠ADC=90°,∴CD∥BQ,
又AD∥BC,∴四边形BCDQ为平行四边形,
∴BC=QD=1,AQ=AD-QD=2-1=1,
∴AQ=QD,即Q为线段AD中点.(6分)
(2)连接AC与BQ交于点N,则N为AC中点,连接![]() ,
,
∵PA∥平面BMQ,∴PA∥MN,
∴M为PC中点,(8分)
∴点M到平面PAB的距离是点C到平面PAB的距离的![]() ,
,
在三棱锥![]() 中,高
中,高![]() ,底面积为
,底面积为![]() ,
,
∴三棱锥![]() 的体积
的体积![]() ,(10分)
,(10分)
又△PAB中,PA=AB=2,PB=![]() ,
,
∴△PAB的面积为![]() .
.
设点M到平面PAB的距离为d,由![]() 可得
可得![]() ,则
,则![]() ,
,
∴点M到平面PAB的距离为![]() .(12分)
.(12分)

【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
(2)由以上统计数据完成下面![]() 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.

附注:
参考数据: ![]() ,
,
参考公式: ![]() ,
, ![]() ,
,
![]() .
.
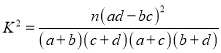
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |