题目内容
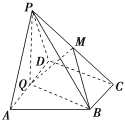
【题目】如图,过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() 分别作直线
分别作直线![]() ,
, ![]() 交椭圆于
交椭圆于![]() 与
与![]() ,且
,且![]() .
.
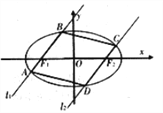
(1)求证:当直线![]() 的斜率
的斜率![]() 与直线
与直线![]() 的斜率
的斜率![]() 都存在时,
都存在时, ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析: (1)设![]() ,分别将
,分别将![]() 坐标代入椭圆中,得出两等式,相减得出
坐标代入椭圆中,得出两等式,相减得出![]() ,写出
,写出![]() 的表达式,化简得出结果; (2)设直线
的表达式,化简得出结果; (2)设直线![]() 的方程
的方程![]() ,联立直线
,联立直线![]() 的方程和椭圆方程,求出
的方程和椭圆方程,求出![]() ,算出
,算出![]() 的表达式,而
的表达式,而![]() ,代入,用基本不等式求出最大值,再得出四边形
,代入,用基本不等式求出最大值,再得出四边形![]() 面积的最大值.
面积的最大值.
试题解析: (1)设![]() ,
, ![]() ,根据对称性,有
,根据对称性,有![]() ,因为
,因为![]() ,
, ![]() 都在椭圆
都在椭圆![]() 上,所以
上,所以![]() ,
, ![]() ,二式相减得,
,二式相减得, ![]() ,所以
,所以![]() 为定值.
为定值.
(2)当![]() 的倾斜角为
的倾斜角为![]() 时,
时, ![]() 与
与![]() 重合,舍去.
重合,舍去.
当![]() 的倾斜角不为0时,由对称性得四边形
的倾斜角不为0时,由对称性得四边形![]() 为平行四边形,
为平行四边形, ![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,得
,得![]() .显然
.显然![]() ,
, ![]() ,
, ![]() .
.
所以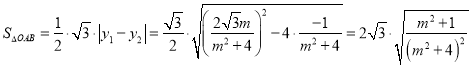
设![]() ,所以
,所以![]() ,
, ![]() .所以
.所以 .
.
当且仅当![]() 即
即![]() 时等号成立,所以
时等号成立,所以![]() .
.
所以平行四边形面积的最大值为![]() .
.
点睛: 本题主要考查直线与椭圆相交时的有关知识,考查学生分析问题解决问题的能力,属于中档题.解题技巧: 在(1)中,采用设而不求;在(2)中, 设直线![]() 的方程
的方程![]() 比
比![]() 好,因为联立直线与椭圆方程计算量减少,还有
好,因为联立直线与椭圆方程计算量减少,还有![]() ,由韦达定理可求出
,由韦达定理可求出![]() .在求三角形
.在求三角形![]() 面积最大值时,将
面积最大值时,将![]() 看成一个整体,利用基本不等式求出最大值.
看成一个整体,利用基本不等式求出最大值.

练习册系列答案
相关题目