题目内容
【题目】如图,在多面体![]() 中,已知四边形
中,已知四边形![]() 为矩形,
为矩形,![]() 为平行四边形,点
为平行四边形,点![]() 在平面
在平面![]() 内的射影恰好为点
内的射影恰好为点![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,且
,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
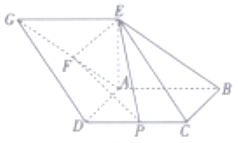
【答案】(1)证明过程如解析所示;(2)![]()
【解析】试题分析:(1)由点E在平面ABCD内的射影恰为A,可得AE⊥平面ABCD,进一步得到平面ABCD⊥平面ABEG,又以BD为直径的圆经过A,C,AD=AB,可得BCD为正方形,再由线面垂直的性质可得BC⊥平面ABEG,从而得到EF⊥BC,结合AB=AE=GE,可得∠ABE=∠AEB=![]() ,从而得到∠AEF+∠AEB=
,从而得到∠AEF+∠AEB=![]() ,有EF⊥BE.再由线面垂直的判定可得EF⊥平面BCE,即平面EFP⊥平面BCE;(2) 连接DE,由(Ⅰ)知,AE⊥平面ABCD,则AE⊥AD,又AB⊥AD,则AB⊥平面ADE,得到GE⊥平面ADE.然后利用等积法求几何体ADC-BCE的体积.
,有EF⊥BE.再由线面垂直的判定可得EF⊥平面BCE,即平面EFP⊥平面BCE;(2) 连接DE,由(Ⅰ)知,AE⊥平面ABCD,则AE⊥AD,又AB⊥AD,则AB⊥平面ADE,得到GE⊥平面ADE.然后利用等积法求几何体ADC-BCE的体积.
试题解析:(1)证明:∵点![]() 在平面
在平面![]() 内的射影恰好为点
内的射影恰好为点![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
∵![]() 为矩形,又平面
为矩形,又平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() ,
,
又![]() 的中点为
的中点为![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 为平行四边形,
为平行四边形,![]() ,
,
∴三棱锥![]() 的高为
的高为![]() ,
,
又![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校从高一年级随机抽取了![]() 名学生第一学期的数学学期综合成绩和物理学期综合成绩.
名学生第一学期的数学学期综合成绩和物理学期综合成绩.
列表如下:
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
规定:综合成绩不低于![]() 分者为优秀,低于
分者为优秀,低于![]() 分为不优秀.
分为不优秀.
对优秀赋分![]() ,对不优秀赋分
,对不优秀赋分![]() ,从
,从![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生,若用
名学生,若用![]() 表示这
表示这![]() 名学生两科赋分的和,求
名学生两科赋分的和,求![]() 的分布列和数学期望;
的分布列和数学期望;
根据这次抽查数据,列出![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为物理成绩与数学成绩有关?
的前提下认为物理成绩与数学成绩有关?
附: 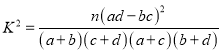 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|