题目内容
【题目】已知f(x)=m(x-2m)(x+m+3),g(x)=2x-2.若同时满足条件:
①x∈R,f(x)<0或g(x)<0;
②x∈(-∞,-4),f(x)g(x)<0,则m的取值范围是 .
【答案】(-4,-2)
【解析】 g(x)=2x4>0 时 x>2
当x﹤1时,g(x)﹤0,
又∵①x∈R,f(x)<0或g(x)﹤0,
∴f(x)=m(x-2m)(x+m+3)<0在x≥1时恒成立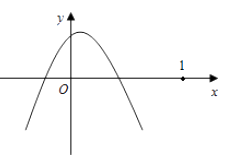
则由二次函数的性质可知开口只能向下,且二次函数与x轴交点都在(1,0)的左面
则
∴-4<m<0,即①成立的范围为-4<m<0
又∵②∈(-∞,-4),f(x) g(x)<0
∴此时g(x)=2x-2<0恒成立
f(x) =m(x-2m)(x+m+3)>0在x∈(-∞,-4)有成立的可能,则只要-4比x1 , x2中的较小的根大即可,
(i)当-1<m<0时,较小的根为-m-3,-m-3<-4不成立
(ii)当m=-1时,两个根同为-2>-4,不成立
(iii)当-4<m<-1时,较小的根为2m,2m<-4,即m<-2成立.
综上可得①②成立时-4<m<-2.
故答案为:(-4,-2)
根据题意当x的取值范围不同时结合指数函数的单调性求解出f(x) >0或f(x) <0的x的解集,进而得到关于m的不等式组解出m的解集即可。

练习册系列答案
相关题目