题目内容
15.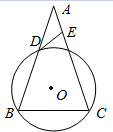 如图,圆O的半径为2,等腰△ABC的底边的两端点B,C在圆O上,AB与圆O交于点D,AD=2,圆O的切线DE交AC于E点.
如图,圆O的半径为2,等腰△ABC的底边的两端点B,C在圆O上,AB与圆O交于点D,AD=2,圆O的切线DE交AC于E点.(I)求证:DE⊥AC;
(Ⅱ)若∠A=30°,求BD的长.
分析 (I)设AC交圆O于点F,则∠B=∠AFD,∠C=∠ADF,证明四边形ADOF是菱形,OD∥AC,即可证明DE⊥AC;
(Ⅱ)作OG⊥BD于点G,则G是BD的中点,DG=ODcos30°,即可求BD的长.
解答  (I)证明:设AC交圆O于点F,则∠B=∠AFD,∠C=∠ADF,
(I)证明:设AC交圆O于点F,则∠B=∠AFD,∠C=∠ADF,
∵∠B=∠C,
∴∠AFD=∠ADF,
∴AD=AF=2,
∵OD=OF=2,
∴四边形ADOF是菱形,
∴OD∥AC,
∵DE为切线,
∴OD⊥DE,
∴DE⊥AC;
(Ⅱ)作OG⊥BD于点G,则G是BD的中点,
∵OD∥AC,
∴∠BDO=∠A=30°,
∴DG=ODcos30°=$\sqrt{3}$,
∴BD=2$\sqrt{3}$.
点评 本题考查圆的切线,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
10.在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量$\overrightarrow{α}$=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为n,其中面积不超过4的平行四边形的个数为m,则$\frac{m}{n}$=( )
| A. | $\frac{4}{15}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
20.已知中心在坐标原点的椭圆和双曲线的焦点相同,左、右焦点分别为F1,F2,这两条曲线在第一象限的交点为P,且△PF1F2是以PF1为斜边的等腰直角三角形,则椭圆和双曲线的离心率之积为( )
| A. | 1 | B. | 2$\sqrt{2}$+3 | C. | 2$\sqrt{2}$ | D. | 3一2$\sqrt{2}$ |
5.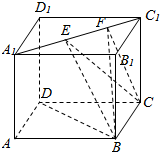 如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
 如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )| A. | BD⊥CE | |
| B. | △CEF的面积为定值 | |
| C. | 四面体BCEF的体积随EF的位置的变化而变化 | |
| D. | 直线BE与CF为异面直线 |
