题目内容
5.已知△ABC及所在平面一点P,符合条件:$\overrightarrow{BP}=\overrightarrow{PC}$,且$\overrightarrow{AP}•\overrightarrow{AB}$=$\overrightarrow{AP}•\overrightarrow{AC}$,则△ABC的形状为( )| A. | 等腰三角形 | B. | 正三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
分析 由$\overrightarrow{BP}=\overrightarrow{PC}$,得到P为BC中点,结合$\overrightarrow{AP}•\overrightarrow{AB}$=$\overrightarrow{AP}•\overrightarrow{AC}$,变形得到AP⊥BC,即AP是BC的垂直平分线,所以AB=AC.
解答 解:因为$\overrightarrow{BP}=\overrightarrow{PC}$,所以BP=PC,
又$\overrightarrow{AP}•\overrightarrow{AB}$=$\overrightarrow{AP}•\overrightarrow{AC}$,
所以$\overrightarrow{AP}•(\overrightarrow{AB}-\overrightarrow{AC})$=0,
即$\overrightarrow{AP}•\overrightarrow{CB}$=0,
所以$\overrightarrow{AP}⊥\overrightarrow{BC}$,
所以AB=AC;
故选A.
点评 本题考查了平面向量的运用;通过向量相等包括方向相同、长度相等;数量积为0,得到向量垂直.

练习册系列答案
相关题目
16.若二项式(2x+$\frac{a}{x}$)7的展开式中$\frac{1}{{x}^{3}}$项的系数是84,则实数a=( )
| A. | 2 | B. | $\root{3}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 1 |
13.若关于实数x的不等式|x-1|+|x-3|≤a2-2a-1的解集为∅,则实数a的取值范围是( )
| A. | a<-1或a>3 | B. | -1<a<3 | C. | -1<a<2 | D. | 1<a<3 |
20.在等差数列{an}中,2a2+a11=6,则数列{an}的前9项和等于( )
| A. | 6 | B. | 12 | C. | 18 | D. | 25 |
 .
. ,求
,求 的值;
的值; 对于
对于 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 则下列结论正确的是( )
则下列结论正确的是( ) 是偶函数 B.
是偶函数 B. 是增函数
是增函数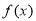 是周期函数 D.
是周期函数 D. 的值域为
的值域为
 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,令
对称,令 ,则关于函数
,则关于函数 有下列命题:
有下列命题: 的图象关于原点对称;
的图象关于原点对称; 上为减函数.
上为减函数.