题目内容
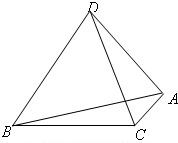
已知a、b为异面直线,点A、B在直线a上,点C、D在直线b上,且AC=AD,BC=BD,则直线a、b所成的角为( )
| A.90° | B.60° | C.45° | D.30° |
取CD的中点E,连结AE、BE
∵△ACD中,AC=AD,E为CD中点,∴AE⊥CD
同理可得BE⊥CD
∵AE、BE是平面ABE内的相交直线
∴CD⊥平面ABE
∵AB?平面ABE,∴CD⊥AB
由此可得AB、CD所成的角为直角,即为异面直线a、b所成的角
所以异面直线a、b所成的角等于90°
故选:A
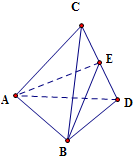
∵△ACD中,AC=AD,E为CD中点,∴AE⊥CD
同理可得BE⊥CD
∵AE、BE是平面ABE内的相交直线
∴CD⊥平面ABE
∵AB?平面ABE,∴CD⊥AB
由此可得AB、CD所成的角为直角,即为异面直线a、b所成的角
所以异面直线a、b所成的角等于90°
故选:A


练习册系列答案
相关题目