题目内容
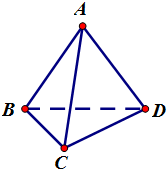
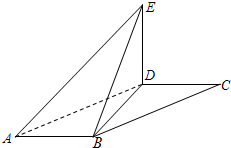
如图,在四边形ABCD中,AB=AD=4,BC=CD=
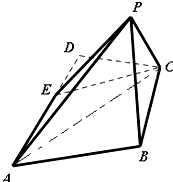
,点E为线段AD上的一点.现将△DCE沿线段EC翻折到PAC,使得平面PAC⊥平面ABCE,连接PA,PB.
(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)若∠BAD=60°,且点E为线段AD的中点,求直线PE与平面ABCE所成角的正弦值.
| 7 |
(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)若∠BAD=60°,且点E为线段AD的中点,求直线PE与平面ABCE所成角的正弦值.

(Ⅰ)证明:连接AC,BD交于点O,在四边形ABCD中,
∵AB=AD=4,BC=CD=
∴△ABC≌△ADC,∴∠DAC=∠BAC,∴AC⊥BD
又∵平面PAC⊥平面ABCE,且平面PAC∩平面ABCE=AC
∴BD⊥平面PAC…(6分)
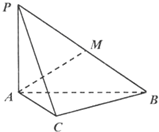
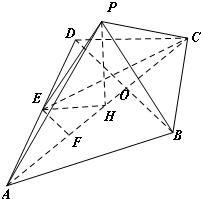
(Ⅱ)如图,过点P作AC的垂线,垂足为H,连接EH,EC,并取AO中点F,连接EF,
∵平面PAC⊥平面ABCE,且平面PAC∩平面ABCE=AC,PH⊥AC
∴PH⊥平面ABCE,∴∠PEH即为直线PE与平面ABCE的所成角,
由(Ⅰ)可知,AC⊥BD,且AO=2
,CO=
,
又PE=2,PC=
,设CH=x,则有PH=
,EH=
=
又∵F为AO的中点,在Rt△EFH中,FH=2
-x,EF=1
由勾股定理得,(2
-x)2+1=x2-3,解得x=
,
∴EH=
,PH=
∴直线PE与平面ABCE的所成角的正弦值即sin∠PEH=
=
.
∵AB=AD=4,BC=CD=
| 7 |
∴△ABC≌△ADC,∴∠DAC=∠BAC,∴AC⊥BD
又∵平面PAC⊥平面ABCE,且平面PAC∩平面ABCE=AC
∴BD⊥平面PAC…(6分)
(Ⅱ)如图,过点P作AC的垂线,垂足为H,连接EH,EC,并取AO中点F,连接EF,
∵平面PAC⊥平面ABCE,且平面PAC∩平面ABCE=AC,PH⊥AC
∴PH⊥平面ABCE,∴∠PEH即为直线PE与平面ABCE的所成角,
由(Ⅰ)可知,AC⊥BD,且AO=2
| 3 |
| 3 |
又PE=2,PC=
| 7 |
| 7-x2 |
| PE2-PH2 |
| x2-3 |
又∵F为AO的中点,在Rt△EFH中,FH=2
| 3 |
由勾股定理得,(2
| 3 |
| 4 |
| 3 |
| 3 |
∴EH=
| 2 |
| 3 |
| 3 |
| 5 |
| 3 |
| 3 |
∴直线PE与平面ABCE的所成角的正弦值即sin∠PEH=
| EH |
| PE |
| ||
| 3 |


练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目