题目内容
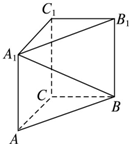
已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,则异面直线BC1与AC所成角的余弦值为______.
连接A1B,设该三棱柱的棱长为1,
∵三棱柱ABC-A1B1C1中,AC∥A1C1
∴∠A1C1B(或其补角)就是异面直线BC1与AC所成的角
∵CC1⊥底面ABC,
∴三棱柱ABC-A1B1C1是直三棱柱,可得四边形B1C1CB是矩形
∵BC=CC1=1,∴BC1=
,同理可得A1B=
△A1C1B中,由余弦定理得:cos∠A1C1B=
=
即异面直线BC1与AC所成角的余弦值为
故答案为:
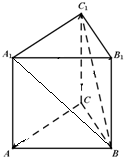
∵三棱柱ABC-A1B1C1中,AC∥A1C1
∴∠A1C1B(或其补角)就是异面直线BC1与AC所成的角
∵CC1⊥底面ABC,
∴三棱柱ABC-A1B1C1是直三棱柱,可得四边形B1C1CB是矩形
∵BC=CC1=1,∴BC1=
| 2 |
| 2 |
△A1C1B中,由余弦定理得:cos∠A1C1B=
| 1+2-2 | ||
2×1×
|
| ||
| 4 |
即异面直线BC1与AC所成角的余弦值为
| ||
| 4 |
故答案为:
| ||
| 4 |


练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

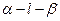 的大小为
的大小为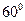 ,
, 为异面直线,且
为异面直线,且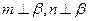 ,则
,则