题目内容
【题目】如图，
是圆柱的直径，
是圆柱的母线，
，
，点
是圆柱底面圆周上的点.
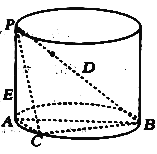
（1）求三棱锥
体积的最大值；
（2）若
，
是线段
上靠近点
的三等分点，点
是线段上的动点，求
的最小值.
【答案】（1）
；（2）4
【解析】
（1）三棱锥的高为定值，要根据三棱锥体积公式
可知，要使得体积最大，就要底面积最大，又因为边
为定值，故当
到的距离取得最大值时，底面积最大，故此时棱锥的体积最大；
（2）反向延长至
，使得
三点共线，三点共线时，距离最短，则
为
最小值.
（1）三棱锥
高
，
，点到的最大值为底面圆的半径
，
则三棱锥体积的最大值等于
.
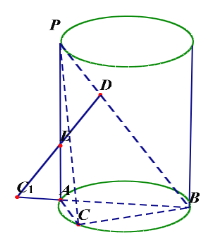
（2）将
绕着
旋转到
使其共面，且在的反向延长线上，连接，与的交点为
，此时最小，为；
由，
，且易知
，由勾股定理知
，因为
，所以
，则
，
；
，则
是边长为4的等边三角形，故
，所以的最小值等于4.
练习册系列答案
相关题目
