题目内容
任意的实数k,直线 与圆
与圆 的位置关系一定是 ( )
的位置关系一定是 ( )
 与圆
与圆 的位置关系一定是 ( )
的位置关系一定是 ( )| A.相离 | B.相切 | C.相交但直线不过圆心 | D.相交且直线过圆心 |
D
试题分析:方法一 利用圆心到直线的距离与半径的大小比较求解
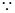 圆
圆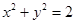 的圆心
的圆心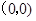 到直线
到直线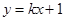 的距离为
的距离为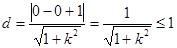 ‘
‘又
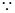
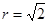 ,
,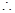
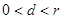 ,
,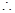 直线与圆相交但直线不过圆心。
直线与圆相交但直线不过圆心。方法二 利用直线方程与圆的方程联立的方程组的根的个求解
联立
 得
得 (*)
(*)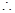
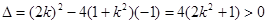
故(*)有两个不等的实数根,所以方程组有两组解,又直线显然过原点
所以直线与圆相交但不过圆心.
点评:解决此类问题的关键是掌握直线与圆的位置关系的判定方法,并能熟练应用。直线与圆的位置关系的判定多用几何法,难度较小。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
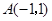 出发经
出发经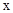 轴反射,到达圆C:
轴反射,到达圆C: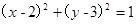 上一点的最短路程是( )
上一点的最短路程是( ) -1
-1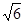
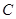 以
以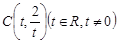 为圆心且经过原点O.
为圆心且经过原点O.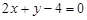 与圆
与圆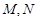 ,若
,若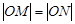 ,求圆
,求圆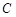 的方程;
的方程;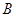 的坐标为
的坐标为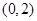 ,设
,设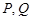 分别是直线
分别是直线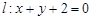 和圆
和圆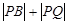 的最小值及此时点
的最小值及此时点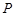 的坐标。
的坐标。 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是  0
0 0
0  0
0 0
0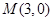 是圆
是圆 :
: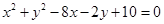 内一点,过
内一点,过 被圆截得的弦最短的直线方程是( )
被圆截得的弦最短的直线方程是( )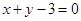
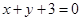

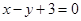
 和
和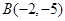 .
. 上,求圆的方程。
上,求圆的方程。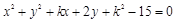 相切,则实数
相切,则实数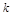 的取值范围是( )
的取值范围是( )
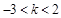
 或
或
 或
或
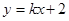 与圆
与圆 有公共点
有公共点 则斜率
则斜率 的取值范围是( )
的取值范围是( )