题目内容
过点(1,2)总可作两条直线与圆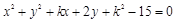 相切,则实数
相切,则实数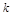 的取值范围是( )
的取值范围是( )
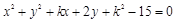 相切,则实数
相切,则实数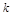 的取值范围是( )
的取值范围是( )A. | B.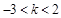 |
C. 或 或 | D. 或 或 |
D
本试题主要是考查了直线与圆的位置关系的运用。
因为把圆的方程化为标准方程得圆心为(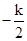 ,-1),半径为16-
,-1),半径为16-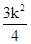 >0,解得
>0,解得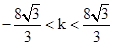 ,又点(1,2)应在已知圆的外部,,把点代入圆方程得:1+4+k+4+k2-15>0,即(k-2)(k+3)>0,,解得:k>2或k<-3,,则实数k的取值范围是
,又点(1,2)应在已知圆的外部,,把点代入圆方程得:1+4+k+4+k2-15>0,即(k-2)(k+3)>0,,解得:k>2或k<-3,,则实数k的取值范围是 或
或 ,选D.
,选D.
解决该试题的关键是点(1,2)应在已知圆的外部,从而得到结论。
因为把圆的方程化为标准方程得圆心为(
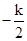 ,-1),半径为16-
,-1),半径为16-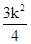 >0,解得
>0,解得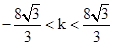 ,又点(1,2)应在已知圆的外部,,把点代入圆方程得:1+4+k+4+k2-15>0,即(k-2)(k+3)>0,,解得:k>2或k<-3,,则实数k的取值范围是
,又点(1,2)应在已知圆的外部,,把点代入圆方程得:1+4+k+4+k2-15>0,即(k-2)(k+3)>0,,解得:k>2或k<-3,,则实数k的取值范围是 或
或 ,选D.
,选D.解决该试题的关键是点(1,2)应在已知圆的外部,从而得到结论。

练习册系列答案
相关题目
 ,动点
,动点 满足
满足 ,则
,则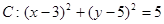 ,过圆心
,过圆心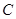 作直线
作直线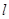 交圆于
交圆于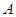 、
、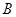 两点,与
两点,与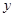 轴交于点
轴交于点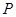 ,若
,若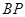 的中点,则直线
的中点,则直线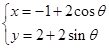 (θ为参数)的位置关系是( )
(θ为参数)的位置关系是( ) 与圆
与圆 的位置关系一定是 ( )
的位置关系一定是 ( )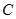 :
: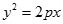 的焦点为圆
的焦点为圆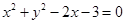 的圆心,直线
的圆心,直线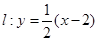 与
与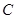 交于不同的两点
交于不同的两点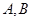 .
.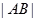 。
。 在圆
在圆 的外部,则实数
的外部,则实数 的范围为___________.
的范围为___________.