题目内容
若圆 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是
 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是 A. 0 0 | B. 0 0 |
C. 0 0 | D. 0 0 |
B
试题分析:∵圆(x-a)2+(y-b)2=b2+1始终平分(x+1)2+(y+1)2=4的周长
∴两圆交点的直线过(x+1)2+(y+1)2=4的圆心(-1,-1)
两圆方程相减可得:(2+2a)x+(2+2b)y-a2-1=0,得到相交弦所在直线,然后
将(-1,-1)代入可得-2-2a-2-2b-a2-1=0,即5+2a+2b+a2=0
故选B
点评:解决该试题的关键是根据圆(x-a)2+(y-b)2=b2+1始终平分(x+1)2+(y+1)2=4的周长,可得两圆交点的直线过(x+1)2+(y+1)2=4的圆心(-1,-1),两圆相减可得公共弦,将(-1,-1)代入可得结论.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 ,直线L:
,直线L: 

 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点; ,动点
,动点 满足
满足 ,则
,则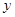 轴相切的圆的标准方程是
轴相切的圆的标准方程是
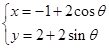 (θ为参数)的位置关系是( )
(θ为参数)的位置关系是( ) ,则这个圆的方程是( )
,则这个圆的方程是( ) 与圆
与圆 的位置关系一定是 ( )
的位置关系一定是 ( ) 作切线,切点为T,则切线长|PT|的最小值是( )
作切线,切点为T,则切线长|PT|的最小值是( )



