题目内容
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
【答案】(1)证明见解析;
(2) ![]() .
.
【解析】
(1)利用题意,证得二面角为![]() ,即可得到平面ACD⊥平面ABC;
,即可得到平面ACD⊥平面ABC;
(2)建立适当的空间直角坐标系,求得两个半平面的法向量,利用向量的夹角公式,即可求解二面角的余弦值。
(1)由题意可得,![]() ,从而
,从而![]() ,
,
又![]() 是直角三角形,所以
是直角三角形,所以![]() ,
,
取AC的中点O,连接DO,BO,则![]() ,
,
又由![]() 是正三角形,所以
是正三角形,所以![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角,
的平面角,
在直角![]() 中,
中,![]() ,
,
又,![]() 所以
所以![]() ,故
,故![]() ,
,
所以平面![]() 平面
平面![]() 。
。
(2)由题设及(1)可知![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,
,
则![]()
由题设知,四面体![]() 的体积为四面体
的体积为四面体![]() 的体积的
的体积的![]() ,从而
,从而![]() 到平面
到平面![]() 的距离为
的距离为![]() 到平面
到平面![]() 的距离的
的距离的![]() ,即
,即![]() 为
为![]() 的中点,得
的中点,得![]() .
.
故![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则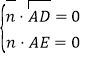 ,即
,即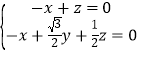 ,
,
令![]() ,则
,则![]() ,即平面
,即平面![]() 的一个法向量
的一个法向量![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则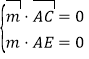 ,
,
可得平面![]() 的一个法向量
的一个法向量![]() ,
,
则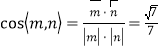 ,即二面角
,即二面角![]() 的余弦值为
的余弦值为![]() 。
。

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案【题目】“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
爱好 | 10 | ||
不爱好 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为![]() ,求
,求![]() 的分布列、数学期望.参考数据:
的分布列、数学期望.参考数据:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024/span> | 6.635 | 7.879 | 10.828 |



