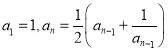题目内容
【题目】质检部门从某超市销售的甲、乙两种食用油中分别随机抽取100桶检测某项质量指标,由检测结果得到如图的频率分布直方图:
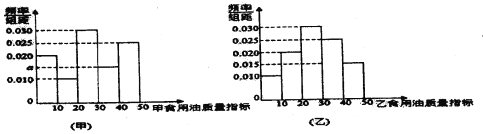
(I)写出频率分布直方图(甲)中![]() 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为![]() ,试比较
,试比较![]() 的大小(只要求写出答案);
的大小(只要求写出答案);
(Ⅱ)佑计在甲、乙两种食用油中各随机抽取1桶,恰有一个桶的质量指标大于20,且另—个桶的质量指标不大于20的概率;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,设
,设![]() 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55, 38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55, 38.45)的桶数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区间的中点值作代表,计算得![]() :
:
②若![]() ,则
,则![]() ,
,![]() .
.
【答案】(1)![]() ;(2)0.42;(3)6.826.
;(2)0.42;(3)6.826.
【解析】
(Ⅰ)由频率分布直方图的矩形面积和为1可得![]() 再由分布的离散程度即可比较方差大小;
再由分布的离散程度即可比较方差大小;
(Ⅱ)设事件A,事件B,事件C,求出P(A),P(B),P(C)即可;
(Ⅲ)求出从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的概率是0.6826,得到X~B(10,0.6826),求出EX即可.
(Ⅰ) ![]() ;
;
(Ⅱ)设事件![]() :在甲公司产品中随机抽取1颗,其质量指标不大于20,
:在甲公司产品中随机抽取1颗,其质量指标不大于20,
事件![]() :在乙公司产品中随机抽取1颗,其质量指标不大于20,
:在乙公司产品中随机抽取1颗,其质量指标不大于20,
事件![]() :在甲、乙公司产品中随机抽各取1颗,恰有一颗糖果的质量指标大于20,且另一个不大于20,则
:在甲、乙公司产品中随机抽各取1颗,恰有一颗糖果的质量指标大于20,且另一个不大于20,则![]() ,
,![]() ,
,
![]()
![]() ;
;
(Ⅲ)计算得: ![]() ,由条件得
,由条件得![]()
从而![]()
![]() ,
,
![]() 从乙公司产品中随机抽取10颗,其质量指标值位于(14.55,38.45)的概率是0.6826,
从乙公司产品中随机抽取10颗,其质量指标值位于(14.55,38.45)的概率是0.6826,
依题意得![]() ,
,
![]() .
.

练习册系列答案
相关题目