题目内容
2．设关于x的不等式x2-x＜2n（n+1）x，（n∈N*）的解集中整数的个数为$\frac{1}{a_n}$，数列{an}的前n项和为Sn，则S100的值为$\frac{50}{101}$．分析 解不等式x2-x＜2n（n+1）x得0＜x＜2n（n+1）+1，从而可得$\frac{1}{a_n}$=2n（n+1），an=$\frac{1}{2n（n+1）}$=$\frac{1}{2}$（$\frac{1}{n}$-$\frac{1}{n+1}$），从而求前100项和即可．
解答 解：∵x2-x＜2n（n+1）x，（n∈N*），
∴x2-（2n（n+1）+1）x＜0，
∴0＜x＜2n（n+1）+1，
∴$\frac{1}{a_n}$=2n（n+1），
∴an=$\frac{1}{2n（n+1）}$=$\frac{1}{2}$（$\frac{1}{n}$-$\frac{1}{n+1}$），
∴S100=$\frac{1}{2}$（1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{100}$-$\frac{1}{101}$）
=$\frac{1}{2}$（1-$\frac{1}{101}$）=$\frac{50}{101}$；
故答案为：$\frac{50}{101}$．
点评 本题考查了二次不等式的求解及裂项求和法的应用，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．某商场为了了解顾客的购物信息，随机的在商场收集了100位顾客购物的相关数据，整理如下：
统计结果显示100位顾客中购物款不低于100元的顾客共60位，据统计该商场每日大约有5000名顾客，为了增加商场销售额度，对一次性购物不低于100元的顾客发放纪念品（每人一件）．
（Ⅰ）试确定m，n的值，并据上述数据估计该商场每日应准备纪念品的数量；
（Ⅱ）若商场进行让利活动，一次购物款200元及以上的一次返利30元；一次性购物款 小于200元的按购物款的百分比返利，具体见下表：
若用各组购物款的中位数估计该组的购物款，请据上述数据估计该商场日均让利多少元？
| 一次购物款（单位：元） | [0，50） | [50，100） | [100，150） | [150，200） | [200，+∞） |
| 顾客人数 | m | 20 | 30 | n | 10 |
（Ⅰ）试确定m，n的值，并据上述数据估计该商场每日应准备纪念品的数量；
（Ⅱ）若商场进行让利活动，一次购物款200元及以上的一次返利30元；一次性购物款 小于200元的按购物款的百分比返利，具体见下表：
| 一次购物款（单位：元） | [0，50） | [50，100） | [100，150） | [150，200） |
| 返利百分比 | 0 | 6% | 8% | 10% |
17．已知函数$f（x）=\frac{1}{1-x}+lnx$，且f（x0）=0，若a∈（1，x0），b∈（x0，+∞），则（ ）
| A． | f（a）＜0，f（b）＜0 | B． | f（a）＞0，f（b）＞0 | C． | f（a）＞0，f（b）＜0 | D． | f（a）＜0，f（b）＞0 |
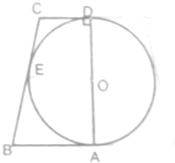如图，半圆O的直径为直角梯形垂直于底的腰，且切AB、BC、CD于A、E、D点，将其绕AD所在直线旋转一周，得到一个球与一个圆台，若球的表面积与圆台侧面积的比为3：4，求球的体积与圆台体积之比．