题目内容
1.(1)已知实数x,y满足不等式x2-2x≥y2-2y,若1≤x≤4,求$\frac{y}{x}$的取值范围;(2)已知函数f(a)=(3m-1)a+b-2m,当m∈[0,1]时,0≤f(a)≤1恒成立,求$\frac{9{a}^{2}+{b}^{2}}{ab}$的取值范围.
分析 (1)由已知求出x,y的约束条件,根据$\frac{y}{x}$的几何意义求范围;
(2)由已知得到a,b的约束条件0≤b-a≤1且0≤2a+b-2≤1利用线性规划问题求出$\frac{b}{a}$的范围,结合基本不等式求范围.
解答 解:(1)∵x2-2x≥y2-2y,
∴(x-y)(x+y-2)≥0,又1≤x≤4
则$\left\{{\begin{array}{l}{x-y≥0}\\{x+y-2≥0}\\{1≤x≤4}\end{array}}\right.$,
对应的平面区域如图,
而$\frac{y}{x}$的几何意义是过区域上的点和原点的直线斜率,所以当过(4,-2)时斜率最小为-$\frac{1}{2}$,在直线y=x时斜率最大为1,
∴$\frac{y}{x}∈[{-\frac{1}{2},1}]$…(6分)
(2)f(a)=g(m)=(3a-2)m+b-a,则g(m)∈[0,1]在m∈[0,1]时恒成立,
∴0≤g(0)≤1且0≤g(1)≤1即$\left\{\begin{array}{l}{0≤b-a≤1}\\{0≤2a+b-2≤1}\end{array}\right.$…(8分)
则由线性规划得a,b对应的平面区域如图
所以$t=\frac{b}{a}∈[{1,4}]$,…(10分)
若$\frac{{9{a^2}+{b^2}}}{ab}=t+\frac{9}{t}$,则$h(t)=t+\frac{9}{t}∈[{6,10}]$
故$\frac{{9{a^2}+{b^2}}}{ab}∈[{6,10}]$…(13分)
点评 本题考查了线性规划的运用;关键是明确x,y的约束条件,利用目标函数的几何意义求范围.

练习册系列答案
相关题目
11.对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:
问:甲、乙谁的平均成绩好?谁的各门功课发展较平衡?( )
| 甲 | 60 | 80 | 70 | 90 | 70 |
| 乙 | 80 | 60 | 70 | 80 | 75 |
| A. | 甲,甲 | B. | 乙,乙 | C. | 甲,乙 | D. | 乙,甲 |
9.等差数列{an}的前n项和为Sn,若a7的值为常数,则下列各数中也是常数的是( )
| A. | S7 | B. | S8 | C. | S13 | D. | S15 |
13.sin1290°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
 满足
满足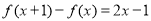 ,且
,且 .
. 的解析式;
的解析式; 时,
时,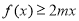 恒成立,求实数
恒成立,求实数 的取值集合.
的取值集合.