题目内容
11.对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:| 甲 | 60 | 80 | 70 | 90 | 70 |
| 乙 | 80 | 60 | 70 | 80 | 75 |
| A. | 甲,甲 | B. | 乙,乙 | C. | 甲,乙 | D. | 乙,甲 |
分析 根据条件分别求出甲乙的平均数和方差进行比较即可.
解答 解:${\overline x_甲}=\frac{1}{5}(60+80+70+90+70)=74$,
${\overline x_乙}=\frac{1}{5}(80+60+70+80+75)=73$,
${s_甲}^2=\frac{1}{5}({14^2}+{6^2}+{4^2}+{16^2}+{4^2})=104$,
${s_乙}^2=\frac{1}{5}({7^2}+{13^2}+{3^2}+{7^2}+{2^2})=56$,
∵${\overline x_甲}>{\overline x_乙},{s_甲}^2>{s_乙}^2$,
∴甲的平均成绩较好,乙的各门功课发展较平衡.
故选:C.
点评 本题考查平均数和方差,对于两组数据一般从稳定程度和平均水平两个方面来观察两组数据,考查学生的计算能力.

练习册系列答案
相关题目
19.过点(1,1),倾斜角为135°的直线截椭圆x2+4y2=4所得的弦长是( )
| A. | $\frac{{2\sqrt{2}}}{5}$ | B. | $\frac{{3\sqrt{2}}}{5}$ | C. | $\frac{{4\sqrt{2}}}{5}$ | D. | $\sqrt{2}$ |
6.已知数列{2n}的前n项和为an,数列{$\frac{1}{{a}_{n}}$}的前n项和为Sn,数列bn的通项公式为bn=(n+1)(n-3),则bnSn的最小值为( )
| A. | -2 | B. | -$\frac{9}{4}$ | C. | -3 | D. | -$\frac{3}{2}$ |
16.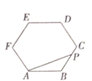 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )
 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )| A. | [-2,6] | B. | [-8,24] | C. | [0,4] | D. | [4,6] |
3.在等差数列{an}中,a2+a5+a8=36,a3+a6+a9=27,则数列{an}的前10项和S10=( )
| A. | 220 | B. | 210 | C. | 110 | D. | 105 |