题目内容
16.已知实数x,y满足$\left\{\begin{array}{l}1≤x-y≤2\\ 2≤x+y≤4\end{array}\right.$,则z=log2(4x+2y+2)的最大值是4.分析 先根据约束条件画出可行域,欲求z=log2(4x+2y+2)的最大值,即要求b=4x+2y+2的最大值,再利用几何意义求最值,分析可得b=4x+2y+2表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最大值即可
解答  解:实数x,y满足$\left\{\begin{array}{l}1≤x-y≤2\\ 2≤x+y≤4\end{array}\right.$对应的平面区域如图,设b=4x+2y+2,
解:实数x,y满足$\left\{\begin{array}{l}1≤x-y≤2\\ 2≤x+y≤4\end{array}\right.$对应的平面区域如图,设b=4x+2y+2,
所以当直线y=-2x-1+$\frac{b}{2}$经过B(3,1)时,b最大,
所以4x+2y+2的最大值为16,
所以z=log2(4x+2y+2)的最大值是:log216=4;
故答案为:4.
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,属于中档题.

练习册系列答案
相关题目
6.已知数列{2n}的前n项和为an,数列{$\frac{1}{{a}_{n}}$}的前n项和为Sn,数列bn的通项公式为bn=(n+1)(n-3),则bnSn的最小值为( )
| A. | -2 | B. | -$\frac{9}{4}$ | C. | -3 | D. | -$\frac{3}{2}$ |
7.下列函数中,既是偶函数又在(0,+∞)上是单调递增函数的是( )
| A. | y=lgx | B. | y=-x2+3 | C. | y=|x|-1 | D. | y=3x |
 (
( 为常数,
为常数,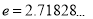 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与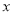 轴平行.
轴平行.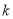 的值;
的值; 的单调区间;
的单调区间; ,其中
,其中 为
为 的导函数.证明:对任意
的导函数.证明:对任意 ,
,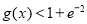 .
.