题目内容
【题目】如果,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 内的一点.
内的一点.
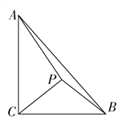
(1)若![]() 是等腰直角三角形
是等腰直角三角形![]() 的直角顶点,求
的直角顶点,求![]() 的长;
的长;
(2)若![]() ,设
,设![]() ,求
,求![]() 的面积
的面积![]() 的解析式,并求
的解析式,并求![]() 的最大值.
的最大值.
【答案】(1)PA=![]() (2)当θ=
(2)当θ=![]() 时,△PBC面积的最大值为
时,△PBC面积的最大值为![]()
【解析】试题分析: ![]() 根据题目条件求出
根据题目条件求出![]() 的大小,根据余弦定理即可求出
的大小,根据余弦定理即可求出![]() ;
;
![]() 在
在![]() 中,根据正弦定理,用含
中,根据正弦定理,用含![]() 的式子表达出
的式子表达出![]() ,
, ![]() ,然后根据
,然后根据
![]() ,可以求出
,可以求出![]() 的解析式,最后根据正弦函数的单调性,可以求出
的解析式,最后根据正弦函数的单调性,可以求出![]() 的最大值。
的最大值。
解析:(1)解法一:∵P是等腰直角三角形PBC的直角顶点,且BC=2,
∴∠PCB=![]() ,PC=
,PC=![]() ,又∵∠ACB=
,又∵∠ACB=![]() ,∴∠ACP=
,∴∠ACP=![]() ,
,
在△PAC中,由余弦定理得PA2=AC2+PC2-2AC·PCcos![]() =5,
=5,
∴PA=![]() .
.
(2)在△PBC中,∠BPC=![]() ,∠PCB=θ,
,∠PCB=θ,
∴∠PBC=![]() -θ,由正弦定理得
-θ,由正弦定理得![]() =
=![]() =
= ,
,
∴PB=![]() sinθ,PC=
sinθ,PC=![]()
![]() ,∴△PBC的面积S(θ)=
,∴△PBC的面积S(θ)=![]() PB·PCsin
PB·PCsin![]()
=![]()
![]() sinθ=2sinθcosθ-
sinθ=2sinθcosθ-![]() sin2θ=sin2θ+
sin2θ=sin2θ+![]() cos2θ-
cos2θ-![]()
=![]()
![]() -
-![]() ,θ∈
,θ∈![]() ,
,
∴当θ=![]() 时,△PBC面积的最大值为
时,△PBC面积的最大值为![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某地最近十年对某商品的需求量逐年上升,下表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
需要量(万件) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量y与年份x之间的回归直线方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)预测该地2018年的商品需求量(结果保留整数).