题目内容
【题目】已知圆C:x2+y2=12,直线l:4x+3y=25,设点A是圆C上任意一点,求点A到直线l的距离小于2的概率.
【答案】
.
【解析】
试题分析：首先与直线l:4x+3y=25平行且到该直线的距离为2的直线为l',且l'与圆C交于P,Q两点. 可求|PQ|=2
,则∠POQ=
，然后利用几何概型的公式即可求得本题答案.
试题解析：由x2+y2=12知,圆心为O(0,0),
∴圆心到直线l的距离d=
=5,
如图所示,设与直线l:4x+3y=25平行且到该直线的距离为2的直线为l',且l'与圆C交于P,Q两点.
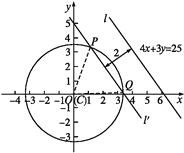
因此点O(0,0)到l'的距离为3,又圆C的半径r=2,
∴在△POQ中,可求|PQ|=2,则∠POQ=.
设“点A到直线l的距离小于2”为事件M,则事件M发生即点A在劣弧
上.
∵劣弧的长为
,∴P(M)=
.
练习册系列答案
相关题目
【题目】汽车是碳排放量比较大的交通工具,某地规定,从2017年开始,将对二氧化碳排放量超过130 g/km的轻型汽车进行惩罚性征税,检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为
=120 g/km.
(1)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性;
(2)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过130 g/km的概率是多少?
