Question

【题目】已知分别是椭圆的左、右焦点，离心率为， 分别是椭圆的上、下顶点， .

(1)求椭圆的方程；

(2)若直线与椭圆交于相异两点，且满足直线的斜率之积为，证明：直线恒过定点，并采定点的坐标.

Answer 1

【答案】（1）（2）直线恒过定点.

【解析】试题分析：（1）设出相关点坐标，利用和离心率为得到几何元素间的关系即可求解；（2）联立直线和椭圆的方程，得到关于的一元二次方程，利用根与系数的关系、斜率公式得到等式，进而利用直线方程判定其过定点.

试题解析：（1）由题知，，，∴，.

∴ ①

由，得 ② 又 ③

由①②③联立解得：

∴椭圆的方程为.

（2）证明：由椭圆的方程得，上顶点，

设，，由题意知，

由得：

∴，

又，，

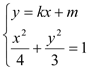由，得，

即：，

∴，

化简得：

解得：，结合知，

即直线恒过定点.