题目内容
【题目】对于R上可导的任意函数f（x），若满足（x﹣2）f′（x）＞0，则必有（ ）
A.f（2）＜f（0）＜f（﹣3）
B.f（﹣3）＜f（0）＜f（2）
C.f（0）＜f（2）＜f（﹣3）
D.f（2）＜f（﹣3）＜f（0）
【答案】A
【解析】解：∵（x﹣2）f′（x）＞0， ∴ 
或 
，
∴x＞2时，f′（x）＞0，x＜0时，f′（x）＜0，
∴f（x）在（﹣∞，2）递减，在（2，+∞）递增，
∵2＞0＞﹣3，
∴f（2）＜f（0）＜f（﹣3），
故选：A．
【考点精析】关于本题考查的利用导数研究函数的单调性，需要了解一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减才能得出正确答案．
练习册系列答案
相关题目
【题目】为了分析某个高三学生的学习状态，对其下一阶段的学习提供指导性建议．现对他前
次考试的数学成绩
、物理成绩
进行分析．下面是该生
次考试的成绩．
88 | 83 | 117 | 92 | 108 | 100 | 112 | |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
（1）他的数学成绩与物理成绩哪个更稳定？请给出你的理由；
（2）已知该生的物理成绩
与数学成绩
是线性相关的，若该生的物理成绩达到
分，请你估计他的数学成绩大约是多少？
（参考公式：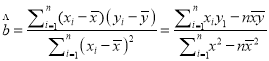 
， 
）
