题目内容
【题目】(Ⅰ)设z=1+i(i是虚数单位),求 ![]() +z2的值; (Ⅱ)设x,y∈R,复数z=x+yi,且满足|z|2+(z+
+z2的值; (Ⅱ)设x,y∈R,复数z=x+yi,且满足|z|2+(z+ ![]() )i=
)i= ![]() ,试求x,y的值.
,试求x,y的值.
【答案】解:(Ⅰ)由z=1+i(i是虚数单位), 则 ![]() +z2=
+z2= ![]() =1﹣i+2i=1+i;
=1﹣i+2i=1+i;
(Ⅱ)把z=x+yi代入|z|2+(z+ ![]() )i=
)i= ![]() ,
,
得 ![]() ,
,
则 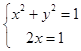 ,解得
,解得 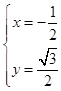 或
或 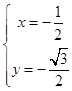
【解析】(Ⅰ)把z=1+i,代入 ![]() +z2 , 然后由复数代数形式的乘除运算化简得答案;(Ⅱ)把Z=x+yi代入|z|2+(z+
+z2 , 然后由复数代数形式的乘除运算化简得答案;(Ⅱ)把Z=x+yi代入|z|2+(z+ ![]() )i=
)i= ![]() ,整理后利用复数相等的条件列式求解x,y的值,则答案可求.
,整理后利用复数相等的条件列式求解x,y的值,则答案可求.
【考点精析】解答此题的关键在于理解复数相等的相关知识,掌握如果两个复数实部相等且虚部相等就说这两个复数相等,以及对复数的乘法与除法的理解,了解设![]() 则
则![]() ;
;![]() .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目