Question

【题目】如图，已知一个八面体各棱长均为1，四边形ABCD为正方形，则下列命题中不正确的是

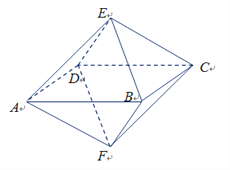
A. 不平行的两条棱所在直线所成的角为或 B. 四边形AECF为正方形

C. 点A到平面BCE的距离为 D. 该八面体的顶点在同一个球面上

Answer 1

【答案】C

【解析】解答：

因为八面体的各条棱长均为1，四边形ABCD为正方形，

所以在四棱锥EABCD中,相邻两条侧棱所成的角为60°,而像AE与CE所成的角为90°，A正确；

因为AE=CE=1,AC= ，满足勾股定理的逆定理，所以AE⊥CE，同理AF⊥CF，AE⊥AF，所以四边形AECF是正方形；故B正确；

设点A到平面BCE的距离h,由VEABCD=2VABCE，

所以 ；

所以点A到平面BCE的距离；故C错误；

该八面体的顶点会在同一个球面上，球心为ABCD的中心，故D正确。

本题选择C选项.