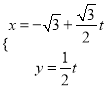题目内容
【题目】选修4-4：坐标系与参数方程
已知圆锥曲线
（
为参数）和定点
，
、
是此圆锥曲线的左、右焦点，以原点
为极点，以
轴的正半轴为极轴建立极坐标系.
（1）求直线
的直角坐标方程；
（2）经过点
且与直线
垂直的直线
交此圆锥曲线于
、
两点，求
的值.
【答案】（1） 
；（2）
.
【解析】
试题分析：（1）将曲线
的参数方程
化为普通方程得
，由此先求出焦点坐标，由直线的截距式求出直线方程即可；（2）由（1）知，直线
的斜率为
，因为
，所以
的斜率为
，所可写出直线
的参数方程，将其参数方程代入椭圆方程，由直线参数的几何意义求之即可.
试题解析：（1）曲线可化为，
其轨迹为椭圆，焦点为
，
.
经过
和
的直线方程为
，即.
（2）由（1）知，直线的斜率为，因为，所以的斜率为，倾斜角为
，
所以的参数方程为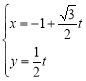
（
为参数）.
代入椭圆
的方程中，得
.
因为
在点
的两侧，所以
.
练习册系列答案
口算题天天练系列答案
相关题目
【题目】已知函数
的定义域为[-1,5]，部分对应值如下表，的导函数
的图象如图所示，下列关于的命题：
| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
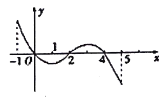
①函数的极大值点为0,4；
②函数在[0,2]上是减函数；
③如果当
时，的最大值是2，那么
的最大值为4；
④当
时，函数
有4个零点.
其中正确命题的序号是__________．
