题目内容
20.函数y=2x的图象经过图象变换得到函数y=4x-3+1的图象,求该坐标变换.分析 先化简函数y=4x-3+1=22x-6+1,由函数y=2x的图象向右平移6个单位,然后横坐标缩短为原来的$\frac{1}{2}$,再向上平移1个单位,得到函数y=22x-6+1的图象.
解答 解:因为y=4x-3+1=22x-6+1,所以只需把y=2x的图象经过下列变换可以得到y=4x-3+1的图象,
(1)先把y=2x的图象向右平移6个单位,得到函数y=2x-6的图象;
(2)再把横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变得到函数y=22x-6的图象;
(3)再把所得函数图象向上平移1个单位即得函数y=4x-3+1的图象.
点评 本题考查直角坐标的变换方法:主要有平移变换和伸缩变换,平移变换改变图象的位置,伸缩变换改变图象的形状或大小,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
11.已知m>0,则m+$\frac{16}{m}$取最小值时,当且仅当m=( )
| A. | 8 | B. | ±4 | C. | 4 | D. | 16 |
9.设扇形的半径长为2cm,面积为4cm2,则扇形的圆心角的弧度数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一个焦点为F,以F为圆心的圆与双曲线的两条渐近线分别相切于 A、B两点,且|AB|=$\sqrt{3}$b,则该双曲线的离心率为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{4}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{10}$ |
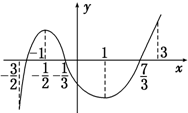 已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].