题目内容
若 是偶函数,它在
是偶函数,它在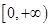 上是减函数,且
上是减函数,且 ,则x的取值范围是( )
,则x的取值范围是( )
A.(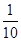 ,1) ,1) | B.(0,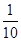 ) ) (1, (1, ) ) |
C.(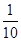 ,10) ,10) | D.(0,1) (10, (10, ) ) |
C
解析试题分析:若lgx>0,则由函数在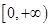 上是减函数,且
上是减函数,且 可得lgx<1,所以
可得lgx<1,所以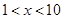 ;若lgx<0,则
;若lgx<0,则 即
即 ,所以-lgx<1,lgx>-1=lg
,所以-lgx<1,lgx>-1=lg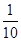 ,所以
,所以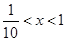 ,而x=1显然成立,故选C。
,而x=1显然成立,故选C。
考点:本题主要考查函数的奇偶性,单调性,对数函数的图象和性质。
点评:综合题,本题也是典型题目,综合考查函数的奇偶性、单调性及对数函数的图象和性质,注意运用已知条件,转化得到x的不等式。

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知函数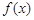 满足:①定义域为R;②
满足:①定义域为R;② ,有
,有 ;③当
;③当 时,
时, .记
.记 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数 的零点个数为 ( )
的零点个数为 ( )
| A.15 | B.10 |
| C.9 | D.8 |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B. | C. | D. |
已知函数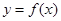 的周期为2,当
的周期为2,当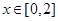 时,
时, ,如果
,如果
 ,则函数
,则函数 的所有零点之和为( )
的所有零点之和为( )
| A.2 | B.4 | C.6 | D.8 |
下列四个函数:(1) (2)
(2) (3)
(3)
(4) ,其中同时满足:①
,其中同时满足:① ②对定义域内的任意两个自变量
②对定义域内的任意两个自变量 ,都有
,都有 的函数个数为
的函数个数为
| A.1 | B.2 | C.3 | D.4 |
函数 和
和 的递增区间依次是( )
的递增区间依次是( )
A.(-∞,0 ,(-∞,1 ,(-∞,1 | B.(-∞,0 ,[1,+∞ ,[1,+∞ |
C.[0,+∞ ,(-∞,1 ,(-∞,1 | D.[0,+∞),[1,+∞) |
已知函数 的零点分别为
的零点分别为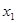 ,
, ,则( )
,则( )
A. | B. |
C. | D. |
定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )
)
使得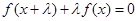 对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“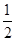 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
对于函数 和
和 ,其定义域为
,其定义域为  .若对于任意的
.若对于任意的 ,总有
,总有 则称
则称 可被
可被 置换,那么下列给出的函数中能置换
置换,那么下列给出的函数中能置换 的是 ( )
的是 ( )
A. | B.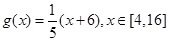 |
C.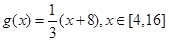 | D. |