题目内容
函数 和
和 的递增区间依次是( )
的递增区间依次是( )
A.(-∞,0 ,(-∞,1 ,(-∞,1 | B.(-∞,0 ,[1,+∞ ,[1,+∞ |
C.[0,+∞ ,(-∞,1 ,(-∞,1 | D.[0,+∞),[1,+∞) |
C
解析试题分析: 递增区间为[0,+∞
递增区间为[0,+∞ ;
; 图象开口向下,对称轴为
图象开口向下,对称轴为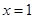 ,其递增区间为(-∞,1
,其递增区间为(-∞,1 ,故选C。
,故选C。
考点:本题主要考查一次函数(分段函数)、二次函数的单调性。
点评:简单题,利用数形结合思想,结合图象知。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知 ,关于
,关于 的方程
的方程 有相异实根的个数情况是( )
有相异实根的个数情况是( )
| A.0或1或2或3 | B.0或1或2或4 |
| C.0或2或3或4 | D.0或1或2或3或4 |
若 是偶函数,它在
是偶函数,它在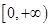 上是减函数,且
上是减函数,且 ,则x的取值范围是( )
,则x的取值范围是( )
A.(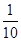 ,1) ,1) | B.(0,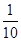 ) ) (1, (1, ) ) |
C.(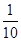 ,10) ,10) | D.(0,1) (10, (10, ) ) |
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |
函数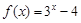 的零点所在区间为( )
的零点所在区间为( )
A.( 1,0) 1,0) | B.(0,1) | C.(1,2) | D.(2,3) |
已知函数 ,正实数
,正实数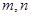 满足
满足 且
且 ,若
,若 在区间
在区间 上的最大值为2,则
上的最大值为2,则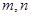 的值分别为
的值分别为
A. ,2 ,2 | B. , ,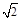 | C. ,2 ,2 | D. ,4 ,4 |
 满足:
满足: 轴对称,并且对任意的
轴对称,并且对任意的
 有
有 ,则当
,则当 时,有( )
时,有( )





 和函数
和函数 的图象如图所示:则函数
的图象如图所示:则函数 的图象可能是
的图象可能是
