题目内容
已知函数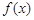 满足:①定义域为R;②
满足:①定义域为R;② ,有
,有 ;③当
;③当 时,
时, .记
.记 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数 的零点个数为 ( )
的零点个数为 ( )
| A.15 | B.10 |
| C.9 | D.8 |
B
解析试题分析:根据题意可知,由于函数f(x),在当 时,
时, ,
,
那么当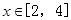 ,则
,则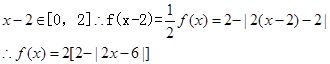
依次作出函数在[4,6],[6,8]的图象,同时能利用函数的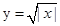 是偶函数的对称性,只要求解出y轴右侧的交点个数,就可以知道共有多少个交点,那么,结合已知中图像的特点可知,交点有5,一共有10个。选B.
是偶函数的对称性,只要求解出y轴右侧的交点个数,就可以知道共有多少个交点,那么,结合已知中图像的特点可知,交点有5,一共有10个。选B.
考点:本试题考查了零点的概念运用。
点评:解决该试题的关键是利用函数的性质,结合函数的给定的绝对值函数的解析式,然后作图,将所求解的 的零点问题转换为函数y=f(x)与函数y=
的零点问题转换为函数y=f(x)与函数y=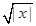 的图像交点个数来解答,这是常用的求零点的方法之一。中档题。
的图像交点个数来解答,这是常用的求零点的方法之一。中档题。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
设 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C.1 | D.3 |
若函数 的零点与
的零点与 的零点之差的绝对值不超过
的零点之差的绝对值不超过 ,则
,则 可以是
可以是
A. | B. |
C. | D. |
已知 ,关于
,关于 的方程
的方程 有相异实根的个数情况是( )
有相异实根的个数情况是( )
| A.0或1或2或3 | B.0或1或2或4 |
| C.0或2或3或4 | D.0或1或2或3或4 |
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,则( )
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
若 是偶函数,它在
是偶函数,它在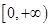 上是减函数,且
上是减函数,且 ,则x的取值范围是( )
,则x的取值范围是( )
A.(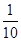 ,1) ,1) | B.(0,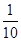 ) ) (1, (1, ) ) |
C.(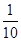 ,10) ,10) | D.(0,1) (10, (10, ) ) |


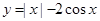 的图象大致是
的图象大致是 
 与
与 (
( 且
且 )的图象可能是( )
)的图象可能是( )



