题目内容
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为 ![]() ,底面是边长为
,底面是边长为 ![]() 的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
A.120°
B.60°
C.45°
D.30°
【答案】B
【解析】解:如图所示, ∵AA1⊥底面A1B1C1 , ∴∠APA1为PA与平面A1B1C1所成角,
∵平面ABC∥平面A1B1C1 , ∴∠APA1为PA与平面ABC所成角.
∵ ![]() =
= ![]() =
= ![]() .
.
∴V三棱柱ABC﹣A1B1C1= ![]() AA1 , 解得AA1=
AA1 , 解得AA1= ![]() .
.
又P为底面正三角形A1B1C1的中心,∴A1P= ![]() =1,
=1,
在Rt△AA1P中,tan∠APA1= ![]() ,
,
∴∠APA1=60°.
故选B.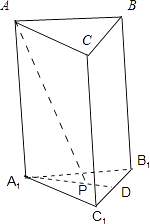
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图: 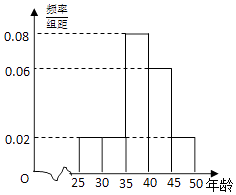
(1)如表是年龄的频数分布表,求a,b的值;
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 50 | 50 | a | 150 | b |
(2)根据频率分布直方图估计志愿者年龄的平均数和中位数;
(3)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的分别抽取多少人?
(4)在(3)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
【题目】从某高中随机选取5名高一男生,其身高和体重的数据如表所示:
身高x(cm) | 160 | 165 | 170 | 175 | 180 |
体重y(kg) | 63 | 66 | 70 | 72 | 74 |
根据如表可得回归方程 ![]() =0.56x+
=0.56x+ ![]() ,据此模型可预报身高为172cm的高一男生的体重为( )
,据此模型可预报身高为172cm的高一男生的体重为( )
A.70.12kg
B.70.29kg
C.70.55kg
D.71.05kg

