题目内容
【题目】一个化肥厂生产甲、乙两种混合肥料，生产1车皮甲种肥料的主要原料是磷酸盐4吨，硝酸盐18吨；生产1车皮乙种肥料需要的主要原料是磷酸盐1吨，硝酸盐15吨．现库存磷酸盐10吨，硝酸盐66吨，在此基础上生产这两种混合肥料．如果生产1车皮甲种肥料产生的利润为12 000元，生产1车皮乙种肥料产生的利润为7 000元，那么可产生的最大利润是（ ）
A.29 000元
B.31 000元
C.38 000元
D.45 000元
【答案】C
【解析】解：设x、y分别表示计划生产甲、乙两种肥料的车皮数． 由题意，得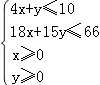 
．
工厂的总利润z=12000x+7000y
由约束条件得可行域如图，
由 
，解得： 
，
所以最优解为A（2，2），
则当直线12000x+7000y﹣z=0过点A（2，2）时，
z取得最大值为：38000元，即生产甲、乙两种肥料各2车皮时可获得最大利润．
故选：C．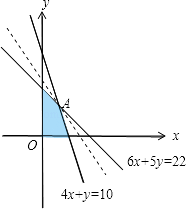
【题目】设函数f（x）=|x﹣a|，a∈R． （Ⅰ）当a=2时，解不等式：f（x）≥6﹣|2x﹣5|；
（Ⅱ）若关于x的不等式f（x）≤4的解集为[﹣1，7]，且两正数s和t满足2s+t=a，求证： 
．
【题目】某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图：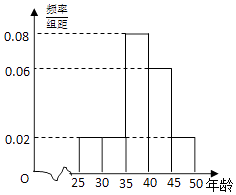 
（1）如表是年龄的频数分布表，求a，b的值；
区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
人数 | 50 | 50 | a | 150 | b |
（2）根据频率分布直方图估计志愿者年龄的平均数和中位数；
（3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的分别抽取多少人？
（4）在（3）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．
【题目】从某高中随机选取5名高一男生，其身高和体重的数据如表所示：
身高x（cm） | 160 | 165 | 170 | 175 | 180 |
体重y（kg） | 63 | 66 | 70 | 72 | 74 |
根据如表可得回归方程 
=0.56x+ 
，据此模型可预报身高为172cm的高一男生的体重为（ ）
A.70.12kg
B.70.29kg
C.70.55kg
D.71.05kg
