题目内容
13.函数f(x)=(x-1)0+(2-x)${\;}^{\frac{1}{2}}$的定义域为{x|x<1或1<x≤2}.分析 利用被开方数非负,以及x-1≠0,即可得到函数的定义域.
解答 解:函数f(x)=(x-1)0+(2-x)${\;}^{\frac{1}{2}}$有意义,可得:$\left\{\begin{array}{l}x-1≠0\\ 2-x≥0\end{array}\right.$,
解得x<1或1<x≤2.
函数f(x)=(x-1)0+(2-x)${\;}^{\frac{1}{2}}$的定义域为:{x|x<1或1<x≤2}.
故答案为:{x|x<1或1<x≤2}.
点评 本题考查函数的定义域的求法,考查计算能力.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
18.已知,a,b,c(a>b>c)是△ABC的角A,B,C的对边,若4sin2(B+C)-3=0,则$\frac{asin(\frac{π}{6}-C)}{b-c}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
5.已知函数f(x)=x+$\frac{a}{x}$+1的值域为(-∞,-1]∪[3,+∞),则a2008=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
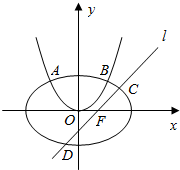 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,椭圆和曲线E:x2=2py(p>0)相交于A、B两点,且M(-$\sqrt{2}$+1,2$\sqrt{2}$),B两点关于直线y=x+$\sqrt{2}$对称.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,椭圆和曲线E:x2=2py(p>0)相交于A、B两点,且M(-$\sqrt{2}$+1,2$\sqrt{2}$),B两点关于直线y=x+$\sqrt{2}$对称.